Global Constraint Catalog: Cbig

5.52. big_valley

DESCRIPTION

LINKS

AUTOMATON

Origin

Derived from $𝚟𝚊𝚕𝚕𝚎𝚢$ .

Constraint

$𝚋𝚒𝚐_𝚟𝚊𝚕𝚕𝚎𝚢 (𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴)$

Arguments

$𝙽$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴$	$𝚒𝚗𝚝$

Restrictions

𝙽 \geq 0

2 * 𝙽 \leq 𝚖𝚊𝚡 (| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1, 0)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴 \geq 0

Purpose

A variable $V_{v}$ ( $1 < k < m$ ) is a valley if and only if there exists an $i$ $(1 < i \leq v)$ such that $V_{i - 1} > V_{i}$ and $V_{i} = V_{i + 1} = \dots = V_{v}$ and $V_{v} < V_{v + 1}$ . Similarly a variable $V_{p}$ ( $1 < p < m$ ) of the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = V_{1}, \dots, V_{m}$ is a peak if and only if there exists an $i$ ( $1 < i \leq p$ ) such that $V_{i - 1} < V_{i}$ and $V_{i} = V_{i + 1} = \dots = V_{p}$ and $V_{p} > V_{p + 1}$ . A valley variable $V_{v}$ ( $1 < v < m$ ) is a potential big valley wrt a non-negative integer $𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴$ if and only if:

$V_{v}$ is a valley,
$\exists i, j \in [1, m] | i < v < j$ , $V_{i}$ is a peak (or $i = 1$ if there is no peak before position $p$ ), $V_{j}$ is a peak (or $i = m$ if there is no peak after position $p$ ), $V_{i} - V_{v} > 𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴$ , and $V_{j} - V_{v} > 𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴$ .

Let $i_{v}$ and $j_{v}$ be the largest $i$ and the smallest $j$ satisfying condition 2. Now a potential big valley $V_{v}$ ( $1 < v < m$ ) is a big valley if and only if the interval $[i, j]$ does not contain any potential big valley that is strictly less than $V_{v}$ . The constraint $𝚋𝚒𝚐_𝚟𝚊𝚕𝚕𝚎𝚢$ holds if and only if $𝙽$ is the total number of big valleys of the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Example

(7, 〈9, 11, 11, 9, 10, 5, 7, 6, 6, 4, 8, 7, 10, 1, 1, 7, 7, 5, 9, 8, 12〉, 0)

(4, 〈9, 11, 11, 9, 10, 5, 7, 6, 6, 4, 8, 7, 10, 1, 1, 7, 7, 5, 9, 8, 12〉, 1)

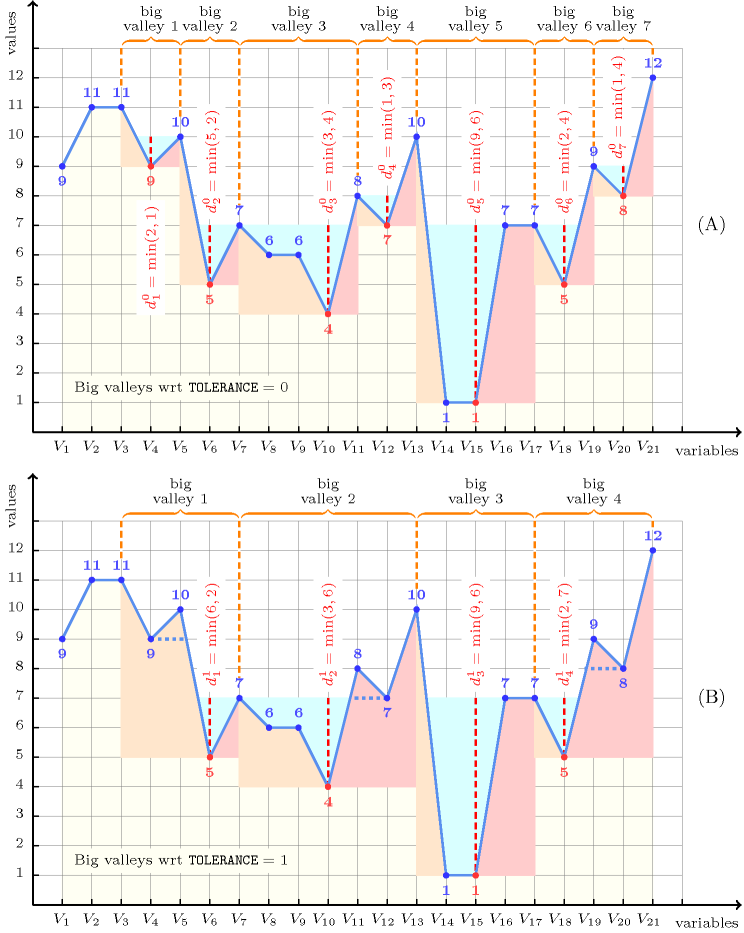
As shown part Part (A) of Figure 5.52.1, the first $𝚋𝚒𝚐_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint holds since the sequence $91111910576648710117759812$ contains seven big valleys wrt a tolerance of 0 (i.e., we consider standard valleys).

As shown part Part (B) of Figure 5.52.1, the second $𝚋𝚒𝚐_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint holds since the same sequence $91111910576648710117759812$ contains only four big valleys wrt a tolerance of 1.

Figure 5.52.1. Illustration of the Example slot: Part (A) a sequence of 21 variables $V_{1}$ , $V_{2}$ , ..., $V_{21}$ respectively fixed to values 9, 11, 11, 9, 10, 5, 7, 6, 6, 4, 8, 7, 10, 1, 1, 7, 7, 5, 9, 8, 12 and its corresponding 7 valleys ( $𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴 = 0$ corresponds to standard valleys) with their respective depths $d_{1}^{0} = 1$ , $d_{2}^{0} = 2$ , $d_{3}^{0} = 3$ , $d_{4}^{0} = 1$ , $d_{5}^{0} = 6$ , $d_{6}^{0} = 2$ , $d_{7}^{0} = 1$ (the left and right hand sides of each valley are coloured in light orange and light red) Part (B) the same sequence of variables and its 4 big valleys when $𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴 = 1$ with their respective depths $d_{1}^{1} = 2$ , $d_{2}^{1} = 3$ , $d_{3}^{1} = 6$ , $d_{4}^{1} = 2$

Typical

𝙽 \geq 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 6

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴 > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Functional dependency: $𝙽$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴$ .
Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙽 = 0$ and $𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴 = 0$ .

Usage

Useful for constraining the number of big valleys of a sequence of domain variables, by ignoring too small peaks that artificially create small valleys wrt $𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴$ .

See also

specialisation: $𝚟𝚊𝚕𝚕𝚎𝚢$ (the tolerance is set to 0 and removed).

Keywords

characteristic of a constraint: automaton, automaton with counters.

combinatorial object: sequence.

constraint arguments: pure functional dependency.

modelling: functional dependency.

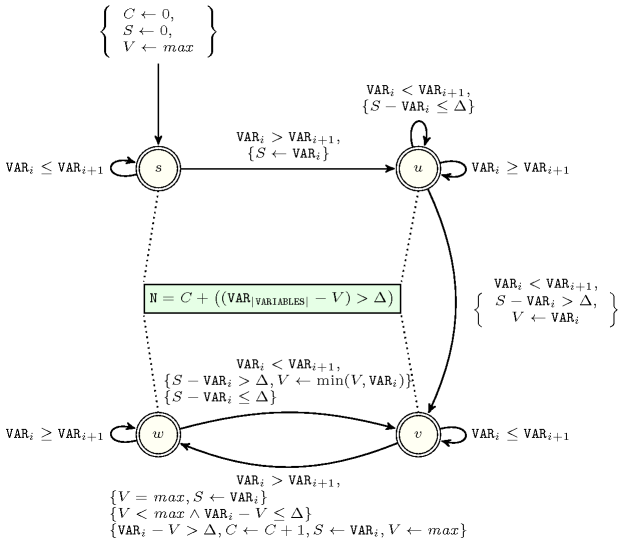
Automaton: Figure 5.52.2 depicts the automaton associated with the $𝚋𝚒𝚐_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint. To each pair of consecutive variables $({𝚅𝙰𝚁}_{i}, {𝚅𝙰𝚁}_{i + 1})$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ , ${𝚅𝙰𝚁}_{i + 1}$ and $S_{i}$ : $({𝚅𝙰𝚁}_{i} < {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 0) \land ({𝚅𝙰𝚁}_{i} = {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 1) \land ({𝚅𝙰𝚁}_{i} > {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 2)$ .

Figure 5.52.2. Automaton for the $𝚋𝚒𝚐_𝚟𝚊𝚕𝚕𝚎𝚢$ where $C$ , $S$ , $V$ , $𝑚𝑎𝑥$ and $Δ$ respectively stand for the number of big valleys already encountered, the altitude at the start of the current potential big valley, the altitude of the current potential big valley, the largest value that can be assigned to a variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ , the $𝚃𝙾𝙻𝙴𝚁𝙰𝙽𝙲𝙴$ parameter

Global Constraint Catalog

5. Global Constraint Catalogue

5.52. big_valley