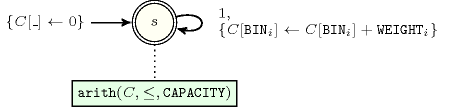5.53. bin_packing
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Given several items of the collection (each of them having a specific weight), and different bins of a fixed capacity, assign each item to a bin so that the total weight of the items in each bin does not exceed .
- Example
-
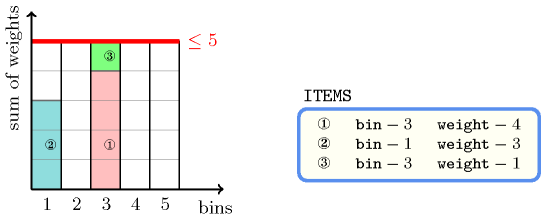
The constraint holds since the sum of the height of items that are assigned to bins 1 and 3 is respectively equal to 3 and 5. The previous quantities are both less than or equal to the maximum 5. Figure 5.53.1 shows the solution associated with the example.
Figure 5.53.1. Bin-packing solution to the Example slot
- Typical
- Symmetries
can be increased.
Items of are permutable.
can be decreased to any value .
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
- Arg. properties
Contractible wrt. .
- Remark
Note the difference with the classical bin-packing problem [MartelloToth90] where one wants to find solutions that minimise the number of bins. In our case each item may be assigned only to specific bins (i.e., the different values of the bin variable) and the goal is to find a feasible solution. This constraint can be seen as a special case of the constraint [AggounBeldiceanu93], where all task durations are equal to 1.
In [Shaw04] the parameter of the constraint is replaced by a collection of domain variables representing the load of each bin (i.e., the sum of the weights of the items assigned to a bin). This allows representing problems where a minimum level has to be reached in each bin.
Coffman and al. give in [CoffmanGareyJohnson84] the worst case bounds of different list algorithms for the bin packing problem (i.e., given a positive integer and a list of integer sizes , what is the smallest integer such that there is a partition satisfying for all ?).
- Algorithm
Initial filtering algorithms are described in [MullerHannemannStilleWeihe03a], [MullerHannemannStilleWeihe03b], [MullerHannemannStilleWeihe03c], [MullerHannemannStilleWeihe03d], [Shaw04]. More recently, linear continuous relaxations based on the graph associated with the dynamic programming approach for knapsack by Trick [Trick03], and on the more compact model introduced by Carvalho [Carvalho99], [Carvalho02] are presented in [CambazardSullivan10].
- Systems
pack in Choco, binpacking in Gecode, bin_packing in MiniZinc.
- See also
generalisation: (fixed overall capacity replaced by non-fixed capacity), (task of 1 replaced by task of given ), ( of 1 replaced by of size 1 with a ), (negative contribution also allowed, fixed capacity replaced by a set of variables).
- Keywords
-
characteristic of a constraint: automaton, automaton with array of counters.
constraint type: resource constraint.
final graph structure: acyclic, bipartite, no loop.
modelling: assignment dimension, assignment to the same set of values.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph class
-
- Sets
-
- Constraint(s) on sets
- Graph model
We enforce the constraint on the weight of the items that are assigned to the same bin.
Parts (A) and (B) of Figure 5.53.2 respectively show the initial and final graph associated with the Example slot. Each connected component of the final graph corresponds to the items that are all assigned to the same bin.
Figure 5.53.2. Initial and final graph of the constraint
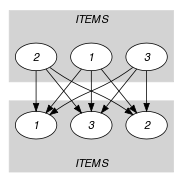
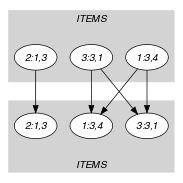
(a) (b)
- Automaton
Figure 5.53.3 depicts the automaton associated with the constraint. To each item of the collection corresponds a signature variable that is equal to 1.
Figure 5.53.3. Automaton of the constraint