5.96. cumulative
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
Cumulative scheduling constraint or scheduling under resource constraints. Consider a set of tasks described by the collection. The constraint enforces that at each point in time, the cumulated height of the set of tasks that overlap that point, does not exceed a given limit. A task overlaps a point if and only if (1) its origin is less than or equal to , and (2) its end is strictly greater than . It also imposes for each task of the constraint .
- Example
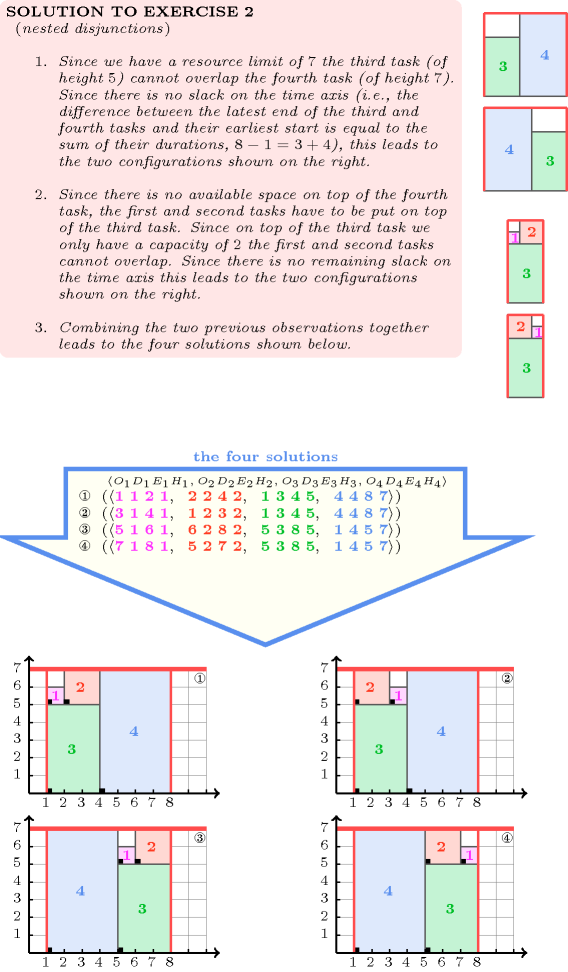
-
Figure 5.96.1. Resource consumption profile corresponding to the five tasks of the Example slot (note that the vertical position of a task does not really matter but is only used for displaying the contribution of a task to the resource consumption profile)
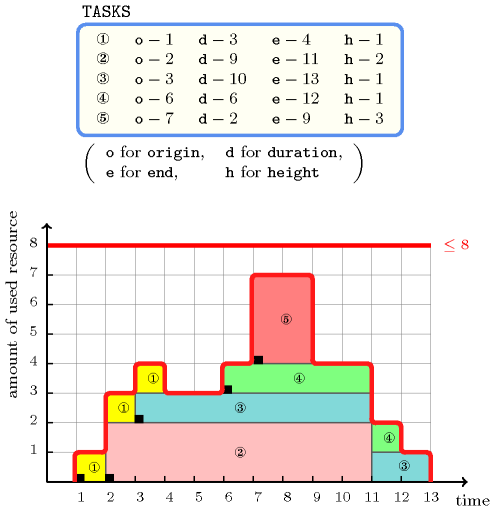
Figure 5.96.1 shows the cumulated profile associated with the example. To each task of the constraint, i.e. each line of the example, corresponds a set of rectangles coloured with the same colour: the sum of the lengths of the rectangles corresponds to the duration of the task, while the height of the rectangles (i.e., all the rectangles associated with a task have the same height) corresponds to the resource consumption of the task. The constraint holds since at each point in time we do not have a cumulated resource consumption strictly greater than the upper limit 8 enforced by the last argument of the constraint.
- All solutions
Figure 5.96.2 gives all solutions to the following non ground instance of the constraint:
, , , ,
, , , ,
, , , ,
, , , ,
.
Figure 5.96.2. All solutions corresponding to the non ground example of the constraint of the All solutions slot
- Typical
- Symmetries
Items of are permutable.
can be decreased to any value .
can be decreased to any value .
One and the same constant can be added to the and attributes of all items of .
can be increased.
- Arg. properties
Contractible wrt. .
- Usage
The constraint occurs in most resource scheduling problems where one has to deal with renewable and/or non-renewable resources:
Renewable resources typically correspond to machines or persons, and tasks require such resources during all their execution (i.e. a resource starts to be used at the beginning of the task and is released at the end of the task). This means that, once a task has finished its work, the resource it was using is available for other tasks. Tasks are defined by their origin, duration, end and resource consumption and can not be interrupted. When the duration and resource consumption are not fixed tasks can be defined by their load, i.e. the product of their duration and resource consumption. To express the dependency between a non-fixed duration/resource consumption of a task with another decision variable (e.g., to state that the duration of a task depends on its start) one can use the constraint where the decision variable corresponds to the index argument of the constraint.
Non renewable resources typically correspond to stock or money, i.e., resources that do not come back when a task finishes to use them. In this context the constraint is used for modelling producer-consumer problems, i.e. problems where a first set of tasks produces a non-renewable resource, while a second set of tasks consumes this resource so that a limit on the minimum or the maximum stock at each instant is imposed.
The constraint is also used as a necessary condition for non-overlapping rectangles (see the constraint).
- Remark
In the original constraint of CHIP the parameter was a domain variable corresponding to the maximum peak of the resource consumption profile. Given a fixed time frame, this variable could be used as a cost in order to directly minimise the maximum resource consumption peak. Fixing this variable is potentially dangerous since it imposes the maximum peak to be equal to a given target value.
Some systems like Ilog CP Optimizer also assume that a zero-duration task overlaps a point if and only if (1) its origin is less than or equal to , and (2) its end is greater than or equal to . Under this definition, the height of a zero-duration task is also taken into account in the resource consumption profile.
Note that the concept of cumulative is different from the concept of rectangles non-overlapping even though, most of the time, each task of a ground solution to a constraint is simply drawn as a single rectangle. As illustrated by Figure 5.118.7, this is in fact not always possible (i.e., some rectangles may need to be broken apart). In fact the constraint is only a necessary condition for rectangles non-overlapping (see Figure 5.118.6 and the corresponding explanation in the Algorithm slot of the constraint).
In MiniZinc (http://www.minizinc.org/) the tasks of a constraint have no attribute.
- Algorithm
The first filtering algorithms were related to the notion of compulsory part of a task [Lahrichi82]. They compute a cumulated resource profile of all the compulsory parts of the tasks and prune the origins of the tasks with respect to this profile in order to not exceed the resource capacity. These methods are sometimes called time tabling. Even though these methods are quite local, i.e., a task has a non-empty compulsory part only when the difference between its latest start and its earliest start is strictly less than its duration, it scales well and is therefore widely used. Later on, more global algorithmsEven though these more global algorithms usually can prune more early in the search tree, these algorithms do not catch all deductions derived from the cumulated resource profile of compulsory parts. based on the resource consumption of the tasks on specific intervals were introduced [ErschlerLopez90], [CaseauLaburthe96b], [Lock96]. A popular variant, called edge finding, considers only specific intervals [MercierVanHentenryck08]. An efficient implementation of edge finding in , where is the number of distinct task heights and is the number of tasks, based on a specific data structure, so called a cumulative -tree [Vilim09a], is provided in [Vilim09b]. When the number of distinct task heights is not small, a usually almost faster implementation in is described in [KameugneFotsoScottNgoKateu11]. A filtering algorithm based on tasks that can not be the earliest (or not be the latest) is described in [SchuttWolf10].
Within the context of linear programming, the reference [HookerYan02] provides a relaxation of the constraint.
A necessary condition for the constraint is obtained by stating a constraint on a subset of tasks such that, for each pair of tasks of , the sum of the two corresponding minimum heights is strictly greater than . This can be done by applying the following procedure:
Let be the smallest minimum height strictly greater than of the tasks of the constraint. If no such task exists then the procedure is stopped without stating any constraint.
Let denote the set of tasks of the constraint for which the minimum height is greater than or equal to . By construction, the tasks of cannot overlap. But we can possibly add one more task as shown by the next step.
When it exists, we can add one task that does not belong to and such that its minimum height is strictly greater than . Again, by construction, this task cannot overlap all the tasks of .
When the tasks are involved in several constraints more sophisticated methods are available for extracting constraints [BaptisteLePape00], [BaptisteDemassey04].
In the context where, both the duration and height of all the tasks are fixed, [BeldiceanuCarlssonPoder08] provides two kinds of additional filtering algorithms that are especially useful when the slack (i.e., the difference between the available space and the sum of the surfaces of the tasks) is very small:
The first one introduces bounds for the so called cumulative longest hole problem. Given an integer that does not exceed the resource limit, and a subset of tasks for which the resource consumption is a most , the cumulative longest hole problem is to find the largest integer such that there is a cumulative placement of maximum height involving a subset of tasks of where, on one interval of the cumulative profile, the area of the empty space does not exceed .
The second one used dynamic programming for filtering so called balancing knapsack constraints. When the slack is 0, such constraints express that the total height of tasks ending at instant must equal the total height of tasks starting at instant . Such constraints can be generalised to non-zero slack.
- Systems
cumulativeMax in Choco, cumulative in Gecode, cumulative in JaCoP, cumulative in MiniZinc, cumulative in SICStus.
- See also
assignment dimension added: (sum of replaced by number of distinct , assignment dimension added), (negative allowed and assignment dimension added).
common keyword: (scheduling constraint), (resource constraint, sum of replaced by number of distinct values), (resource constraint), (resource constraint, defined by a set of ), (resource constraint, sum of replaced by product of ), (resource constraint, a constraint for each set of having a priority less than or equal to a given threshold).
generalisation: ( replaced by with a ).
implied by: ( is a neccessary condition for each dimension of the constraint).
related: , (lexicographic ordering on the origins of , , ), (controlling the shape of the cumulative profile for breaking symmetry).
specialisation: ( replaced by ), (all have a of 1 and a fixed ), (all have a of 1), (all have the same equal to and the same equal to 1).
- Keywords
characteristic of a constraint: core, automaton, automaton with array of counters.
complexity: sequencing with release times and deadlines.
constraint type: scheduling constraint, resource constraint, temporal constraint.
filtering: linear programming, dynamic programming, compulsory part, cumulative longest hole problems, Phi-tree.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph class
-
- Sets
-
- Constraint(s) on sets
- Graph model
The first graph constraint forces for each task the link between its origin, its duration and its end. The second graph constraint makes sure, for each time point corresponding to the start of a task, that the cumulated heights of the tasks that overlap does not exceed the limit of the resource.
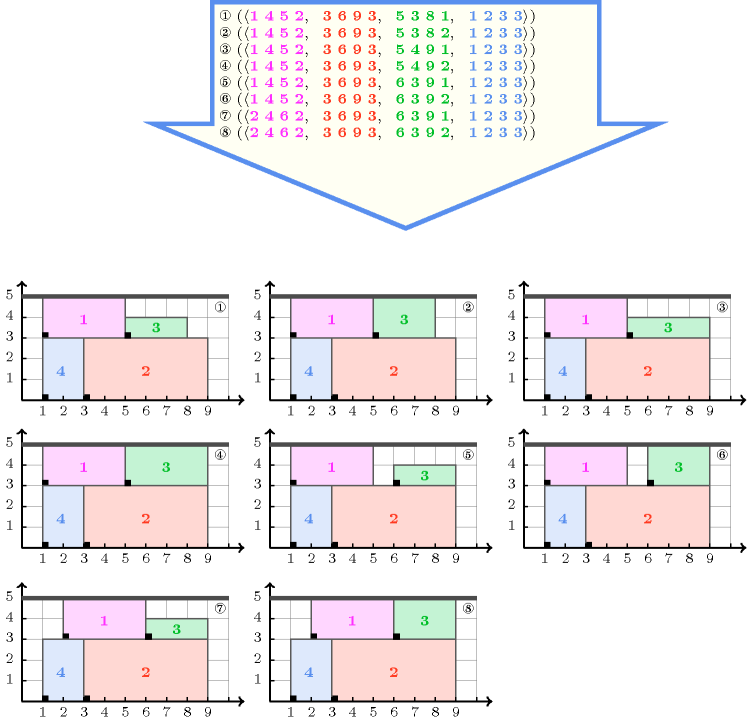
Parts (A) and (B) of Figure 5.96.3 respectively show the initial and final graph associated with the second graph constraint of the Example slot. On the one hand, each source vertex of the final graph can be interpreted as a time point. On the other hand the successors of a source vertex correspond to those tasks that overlap that time point. The constraint holds since for each successor set of the final graph the sum of the heights of the tasks in does not exceed the limit .
Figure 5.96.3. Initial and final graph of the constraint
(a) 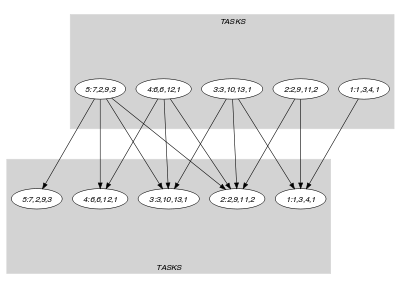
(b) - Signature
Since is the maximum number of vertices of the final graph of the first graph constraint we can rewrite to . This leads to simplify to .
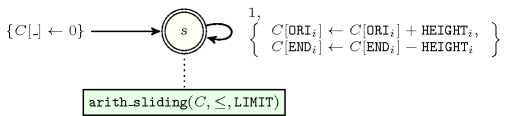
- Automaton
Figure 5.96.4 depicts the automaton associated with the constraint. To each item of the collection corresponds a signature variable that is equal to 1.
Figure 5.96.4. Automaton of the constraint
- Quiz
: checking whether a ground instance holds or not

: finding all solutions