5.103. cycle
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Consider a digraph described by the collection. is equal to the number of circuits for covering in such a way that each vertex of belongs to a single circuit. can also be interpreted as the number of cycles of the permutation associated with the successor variables of the collection.
- Example
-
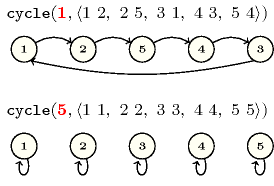
In the first example we have the following 2 () cycles: and . Consequently, the corresponding constraint holds.
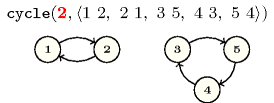
In the second example we have 1 () cycle: .
In the third example we have the following 5 () cycles: , , , and .
- All solutions
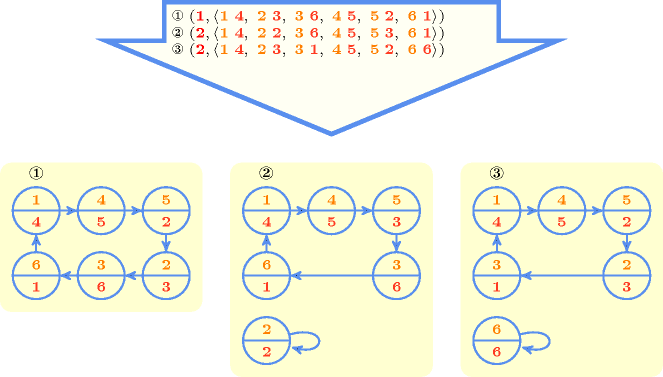
Figure 5.103.1 gives all solutions to the following non ground instance of the constraint: , , , , , , , .
Figure 5.103.1. All solutions corresponding to the non ground example of the constraint of the All solutions slot
- Typical
- Symmetries
Items of are permutable.
Attributes of are permutable w.r.t. permutation (permutation applied to all items).
- Arg. properties
Functional dependency: determined by .
- Usage
The PhD thesis of Éric Bourreau [Bourreau99] mentions the following applications of extensions of the constraint:
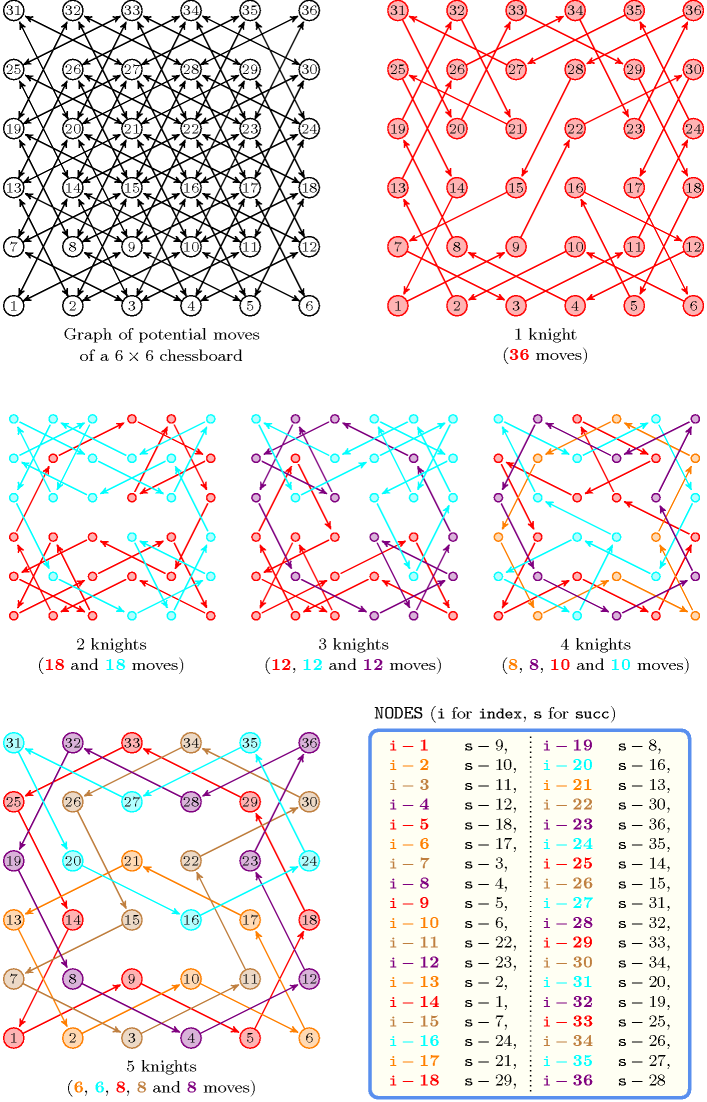
The balanced Euler knight problem where one tries to cover a rectangular chessboard of size by knights that all have to visit between and distinct locations. For some values of , and there does not exist any solution to the previous problem. This is for instance the case when . Figure 5.103.2 depicts the graph associated with the chessboard as well as examples of balanced solutions with respectively 1, 2, 3, 4 and 5 knights.
Some pick-up delivery problems where a fleet of vehicles has to transport a set of orders. Each order is characterised by its initial location, its final destination and its weight. In addition one also has to take into account the capacity of the different vehicles.
Figure 5.103.2. Graph of potential moves of a chessboard, corresponding balanced knight's tours with 1 up to 5 knights, and collection of nodes passed to the constraint corresponding to the solution with 5 knights; note that their is no balanced knight's tour on a chessboard where each knight exactly performs 6 moves.
- Remark
In the original constraint of CHIP the attribute was not explicitly present. It was implicitly defined as the position of a variable in a list.
In an early version of the CHIP there was a constraint named that, from a declarative point of view, was equivalent to . In ALICE [Lauriere78] the constraint was also present.
Given a complete digraph of vertices as well as an unrestricted number of circuits , the total number of solutions to the corresponding constraint corresponds to the sequence A000142 of the On-Line Encyclopaedia of Integer Sequences [Sloane10]. Given a complete digraph of vertices as well as a fixed number of circuits between 1 and , the total number of solutions to the corresponding constraint corresponds to the so called Stirling number of first kind.
- Algorithm
Since all variables have to take distinct values one can reuse the algorithms associated with the constraint. A second necessary condition is to have no more than strongly connected components. Pruning for enforcing this condition, as soon as we have strongly connected components, can be done by forcing all strong bridges to belong to the final solution, since otherwise we would have more than strongly connected components. Since all the vertices of a circuit belong to the same strongly connected component an arc going from one strongly connected component to another strongly connected component has to be removed.
- Reformulation
-
Let and respectively denotes the number of vertices (i.e., ) and the successor variables associated with vertices . The constraint can be reformulated as a conjunction of one constraint, constraints, constraints, and one constraint.
First, we state an
constraint for enforcing distinct values to be assigned to the successor variables.
Second, the key idea is to extract for each vertex (with ) all the vertices that belong to the same cycle. This is done by stating a conjunction of constraints of the form:
Then, using a constraint, we get a unique representative for the cycle containing vertex .
Third, using a constraint, we get the number of distinct cycles.

- Counting
-
Length () 2 3 4 5 6 7 8 9 10 Solutions 2 6 24 120 720 5040 40320 362880 3628800 Number of solutions for : domains
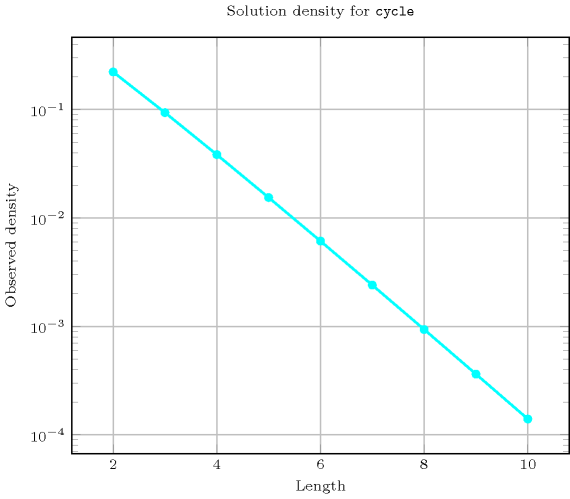
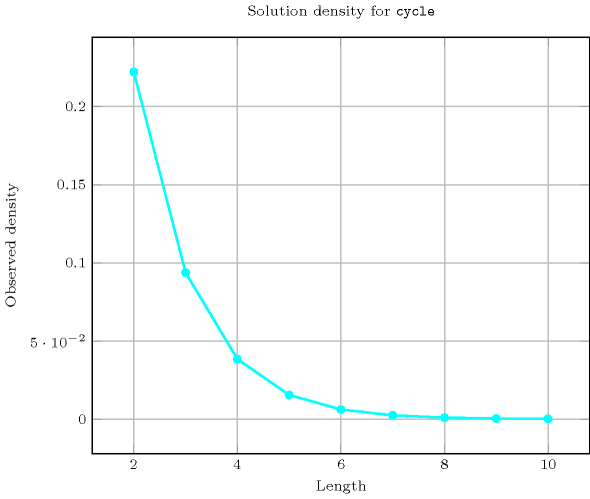
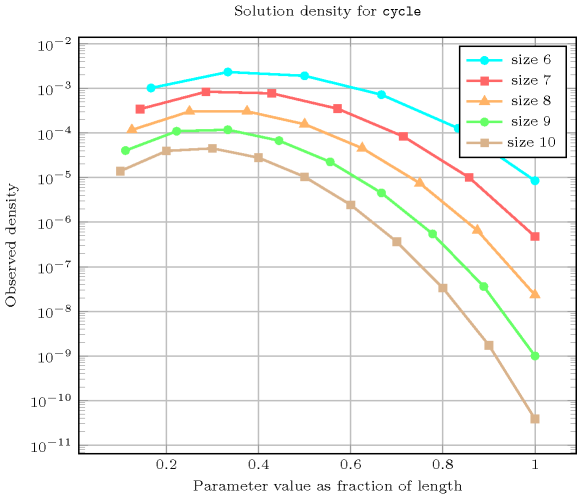
Length () 2 3 4 5 6 7 8 9 10 Total 2 6 24 120 720 5040 40320 362880 3628800 Parameter value 1 1 2 6 24 120 720 5040 40320 362880 2 1 3 11 50 274 1764 13068 109584 1026576 3 - 1 6 35 225 1624 13132 118124 1172700 4 - - 1 10 85 735 6769 67284 723680 5 - - - 1 15 175 1960 22449 269325 6 - - - - 1 21 322 4536 63273 7 - - - - - 1 28 546 9450 8 - - - - - - 1 36 870 9 - - - - - - - 1 45 10 - - - - - - - - 1 Solution count for : domains
- See also
common keyword: (permutation),
(permutation,graph partitioning constraint),
(graph partitioning constraint),
(permutation),
(graph constraint,graph partitioning constraint),
(permutation),
(graph partitioning constraint),
(permutation),
(graph partitioning constraint).
implies: .
implies (items to collection): .
related: (counting number of cycles versus controlling how balanced the cycles are).
specialisation: ( set to 1).
used in reformulation: , , , .
- Keywords
characteristic of a constraint: core.
combinatorial object: permutation.
constraint arguments: business rules.
constraint type: graph constraint, graph partitioning constraint.
filtering: strong bridge, DFS-bottleneck.
final graph structure: circuit, connected component, strongly connected component, one_succ.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
From the restrictions and from the arc constraint, we deduce that we have a bijection from the successor variables to the values of interval . With no explicit restrictions it would have been impossible to derive this property.
In order to express the binary constraint that links two vertices one has to make explicit the identifier of the vertices. This is why the constraint considers objects that have two attributes:
One fixed attribute that is the identifier of the vertex,
One variable attribute that is the successor of the vertex.
The graph property 0 is used in order to avoid having vertices that both do not belong to a circuit and have at least one successor located on a circuit. This concretely means that all vertices of the final graph should belong to a circuit.
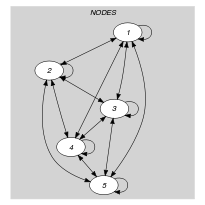
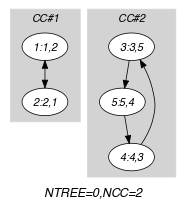
Parts (A) and (B) of Figure 5.103.3 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property, we show the two connected components of the final graph. The constraint holds since all the vertices belong to a circuit (i.e., 0) and since 2.
Figure 5.103.3. Initial and final graph of the constraint
(a) (b) - Quiz
: checking whether a ground instance holds or not

: finding all solutions

: identifying infeasible values

: variable-based degree of violation

: De Bruijn sequence