5.118. diffn
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, , , .
- Type
- Argument
- Restrictions
- Purpose
Generalised multi-dimensional non-overlapping constraint: Holds if, for each pair of orthotopes , and do not overlap. Two orthotopes do not overlap if one of the orthotopes has zero size or if there exists at least one dimension where their projections do not overlap.
- Example
-
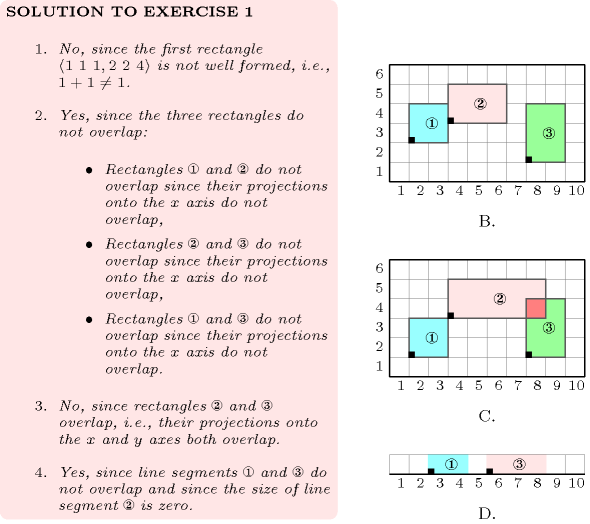
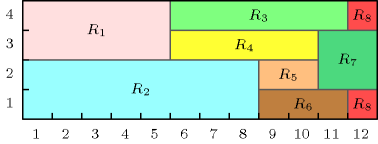
Figure 5.118.1 represents the position of the three rectangles of the example. The coordinates of the leftmost lowest corner of each rectangle are stressed in bold. The constraint holds since the three rectangles do not overlap as explained in Figure 5.118.2.
Figure 5.118.1. Illustration of the Example slot: the three rectangles
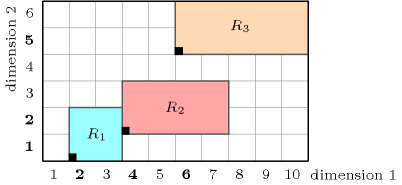
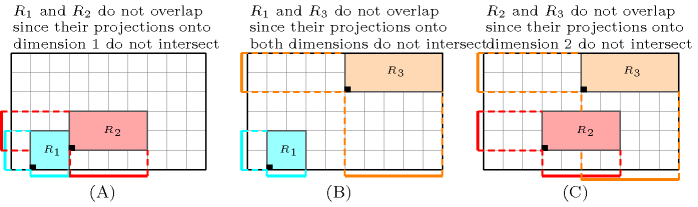
Figure 5.118.2. Illustration of the Example slot: the reasons (A), (B), (C) why the pairs of rectangles , , do not overlap
- All solutions
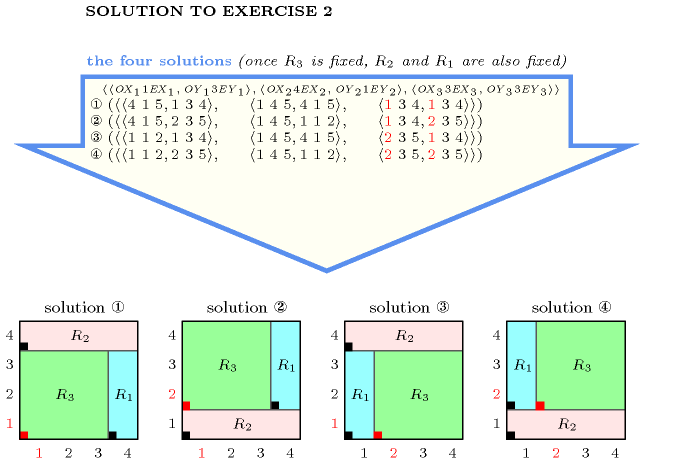
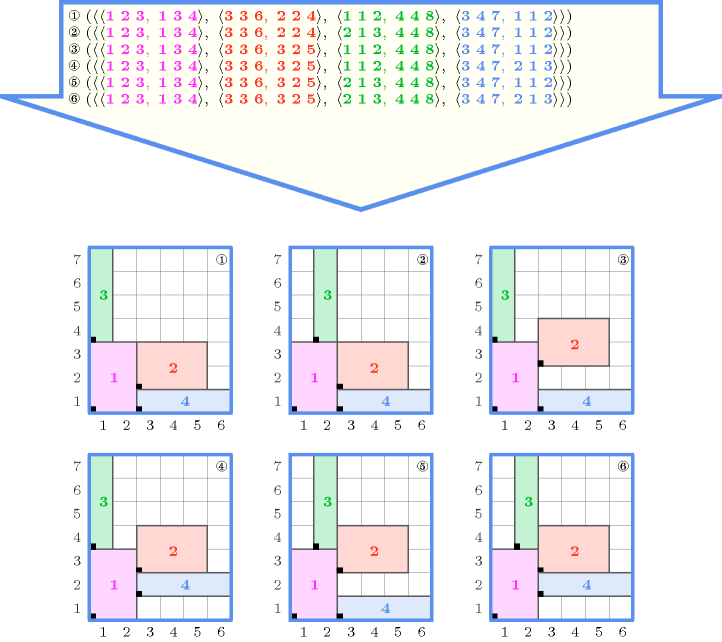
Figure 5.118.3 gives all solutions to the following non ground instance of the constraint:
, , , ,
, , , ,
, , , ,
, , , ,
.
Figure 5.118.3. All solutions corresponding to the non ground example of the constraint of the All solutions slot
- Typical
- Symmetries
Items of are permutable.
Items of are permutable (same permutation used).
can be decreased to any value .
One and the same constant can be added to the and attributes of all items of .
- Arg. properties
Contractible wrt. .
- Usage
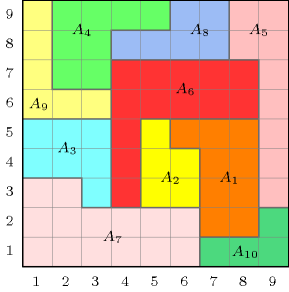
The constraint occurs in placement and scheduling problems. It was for instance used for scheduling problems where one has to both assign each non-preemptive task to a resource and fix its origin so that two tasks, which are assigned to the same resource, do not overlap. When the resource is a set of persons to which non-preemptive tasks have to be assigned this corresponds to so called timetabling problems. A second practical application from the area of the design of memory-dominated embedded systems [Szymanek04] can be found in [SzymanekKuchcinski01]. Together with arithmetic and constraints, the constraint was used in [Szczygiel01] for packing more complex shapes such as angles. Figure 5.118.4 illustrates the angle packing problem on an instance involving 10 angles taken from [Szczygiel01].
Figure 5.118.4. A solution for the angle packing problem of items , , , , , , , , , .
One other packing problem attributed to S. Golomb is to find the smallest square that can contain the set of consecutive squares from up to so that these squares do not overlap each other (see the smallest rectangle area problem).
- Remark
Unlike the definition of the Purpose slot the original paper [BeldiceanuContejean94] introducing the constraint imposes all orthotopes sizes to be different from 0. But it is convenient to allow variable sizes which can be assigned value 0 to model the fact that an orthotope can be skipped.
When we have segments (respectively rectangles) the constraint is referenced under the name (respectively ) in SICStus Prolog [Sicstus95]. When we have rectangles the constraint is also called in JaCoP. In MiniZinc (http://www.minizinc.org/) the constraint considers only rectangles.
It was shown in [Thiel04] that, finding out whether a non-overlapping constraint between a set of rectangles has a solution or not is NP-hard. This was achieved by reduction from sequencing with release times and deadlines.
In the two-dimensional case, when rectangles heights are all equal to one and when rectangles starts in the first dimension are all fixed, the constraint can be rewritten as a constraint corresponding to a system of constraints derived from the maximum cliques of the corresponding interval graph.
- Algorithm
Checking whether a constraint for which all variables are fixed is satisfied or not is related to the Klee's measure problem: given a collection of axis-aligned multi-dimensional boxes, how quickly can one compute the volume of their union. Then the constraint holds if the volume of the union is equal to the sum of the volumes of the different boxes.
A first possible method for filtering non zero size orthotopes is to use constructive disjunction. The idea is to try out each alternative of a disjunction (e.g., given two orthotopes and that should not overlap, we successively assume for each dimension that finishes before , and that finishes before ) and to remove values that were pruned in all alternatives. For the two-dimensional case of a second possible solution used in [RochonDuVerdier92] is to represent explicitly the two-dimensional domain of the origin of each rectangle by a quadtree [Samet89] and to accumulate all forbidden regions within this data structure. As for conventional domain variables, a failure occurs when a two-dimensional domain get empty. A third possible filtering algorithm based on sweep is described in [BeldiceanuCarlsson01sweep].
The thesis of J. Nelissen [Nelissen94] considers the case where all rectangles have the same size and can be rotated from 90 degrees (i.e., the pallet loading problem.). For the -dimensional case of a filtering algorithm handling the fact that two objects do not overlap is given in [BeldiceanuGuoThiel01].
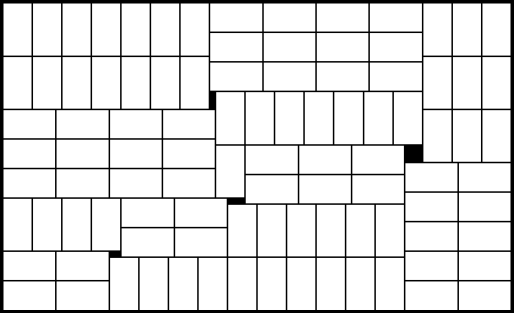
Figure 5.118.5. A hard instance from [Nelissen94]: A solution for packing 99 rectangles of size into a rectangle of size
Extensions of the non-overlapping constraint to polygons and to more complex shapes are respectively described in [BeldiceanuGuoThiel01] and in [RibeiroCarravilla04]. Specialised propagation algorithms for the squared squares problem [BouwkampDuijvestijn92] (based on the fact that no waste is permitted) are given in [Gambini99a] and in [Gambini99b].
The constraint can be used as a necessary condition for the constraint. Figure 5.118.6 illustrates this point for the two-dimensional case. A first (respectively second) constraint is obtained by forgetting the -coordinate (respectively the -coordinate) of the origin of each rectangle occurring in a constraint. Parts (B) and (C) respectively depict the cumulated profiles associated with the projection of the rectangles depicted by part (A) on the and axes.
The constraint is a necessary but not sufficient condition for the two-dimensional case of the constraint. Figure 5.118.7 illustrates this point on an example taken from [Biro90] where one has to place the 8 rectangles , , , , , , , of respective size , , , , , , and in a big rectangle of size . As shown by Figure 5.118.7 there is a cumulative solution where is split in two parts but M. Hujter proves in [Hujter90] that there is no solution where no rectangle is split.
Figure 5.118.6. Looking from the perspective of the constraint in a two-dimensional rectangles placement problem: projecting the three rectangles of (A) on the axis (B) and on the axis (C)
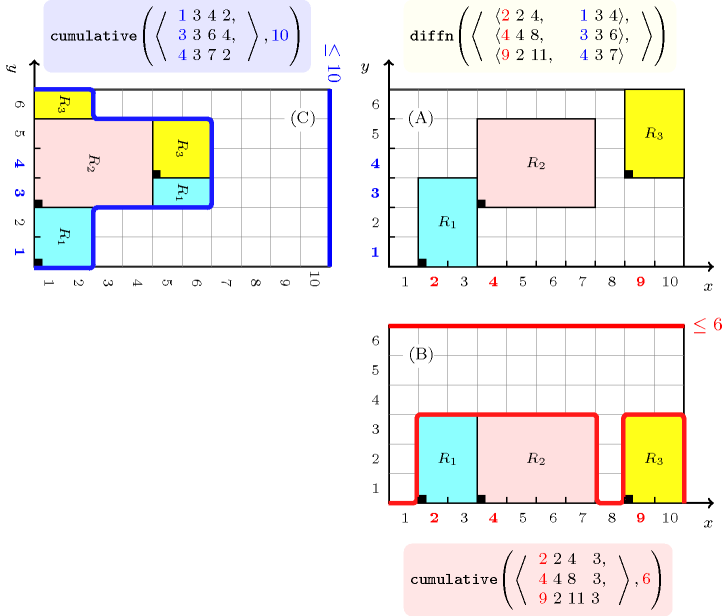
Figure 5.118.7. Illustrating the necessary but not sufficient placement condition: the rectangle is split in two parts
In the context of parallelepipeds that have to be packed [GehringMenschnerMeyer90], [LiCheng90] within a box of sizes one can proceed as follows for stating three constraints. The (with ) parallelepiped is described by the following attributes:
, , (with ) the coordinates of its origin on the , and -axes.
, , (with ) its sizes on the , and -axes.
, , (with ) the surfaces of its projections onto the planes , , and respectively equal to , , and .
its volume (equal to ).
For the placement of parallelepipeds we get the following necessary conditions that respectively correspond to three constraints on the planes , , and :
- Reformulation
Based on the fact that two orthotopes do not overlap if there exists at least one dimension where their projections do not overlap one can reformulate the constraint as a disjunction of inequalities between the origin and the end attributes. In addition one has to link the origin, the size and the end attributes of each orthotope in each dimension.
If we consider the example described in the Example slot we get the following reformulation:
(link between the origin, size and end in dimension 1 of the first orthotope),
(link between the origin, size and end in dimension 2 of the first orthotope),
(link between the origin, size and end in dimension 1 of the second orthotope),
(link between the origin, size and end in dimension 2 of the second orthotope),
(link between the origin, size and end in dimension 1 of the third orthotope),
(link between the origin, size and end in dimension 2 of the third orthotope),
(non-overlapping between the first and second orthotopes),
(non-overlapping between the first and third orthotopes),
(non-overlapping between the second and third orthotopes).
- Systems
geost in Choco, nooverlap in Gecode, diff2 in JaCoP, diff in JaCoP, disjoint in JaCoP, disjointconditional in JaCoP, diffn in MiniZinc.
- Used in
- See also
common keyword: (multi-site employee scheduling with calendar constraints,
scheduling with machine choice, calendars and preemption), , (geometrical constraint,orthotope), , , (geometrical constraint,non-overlapping), (geometrical constraint).
implies: (implies one constraint for each dimension).
related: ( is a necessary condition for : forget one dimension when the number of dimensions is equal to 3), , (lexicographic ordering on the origins of , , ), , .
specialisation: ( replaced by , of same length), ( replaced by ), ( replaced by with and attributes), (orthotope replaced by of 1), (when rectangles heights are all equal to 1 and rectangles starts in the first dimension are all fixed), ( replaced by ).
- Keywords
application area: floor planning problem.
characteristic of a constraint: core.
combinatorial object: pentomino.
complexity: sequencing with release times and deadlines.
constraint arguments: business rules.
constraint type: decomposition, timetabling constraint, relaxation.
filtering: Klee measure problem, sweep, quadtree, compulsory part, constructive disjunction, SAT.
geometry: geometrical constraint, orthotope, polygon, non-overlapping.
heuristics: heuristics for two-dimensional rectangle placement problems.
modelling: disjunction, assignment dimension, assignment to the same set of values, assigning and scheduling tasks that run in parallel, relaxation dimension, sequence dependent set-up, multi-site employee scheduling with calendar constraints, scheduling with machine choice, calendars and preemption.
modelling exercises: assignment to the same set of values, assigning and scheduling tasks that run in parallel, relaxation dimension, sequence dependent set-up, multi-site employee scheduling with calendar constraints, scheduling with machine choice, calendars and preemption.
problems: strip packing, two-dimensional orthogonal packing, pallet loading.
puzzles: squared squares, packing almost squares, Partridge, pentomino, Shikaku, smallest square for packing consecutive dominoes, smallest square for packing rectangles with distinct sizes, smallest rectangle area, Conway packing problem.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
The constraint is expressed by using two graph constraints:
The first graph constraint forces for each dimension and for each orthotope the link between the corresponding , and attributes.
The second graph constraint imposes each pair of distinct orthotopes to not overlap.
Parts (A) and (B) of Figure 5.118.8 respectively show the initial and final graph associated with the second graph constraint of the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold.
Figure 5.118.8. Initial and final graph of the constraint
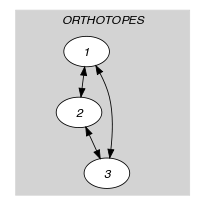
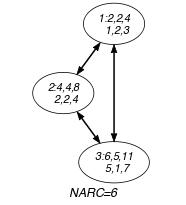
(a) (b) - Signature
Since is the maximum number of vertices of the final graph of the first graph constraint we can rewrite to . This leads to simplify to .
Since we use the arc generator on the collection, is the maximum number of vertices of the final graph of the second graph constraint. Therefore we can rewrite to . Again, this leads to simplify to .
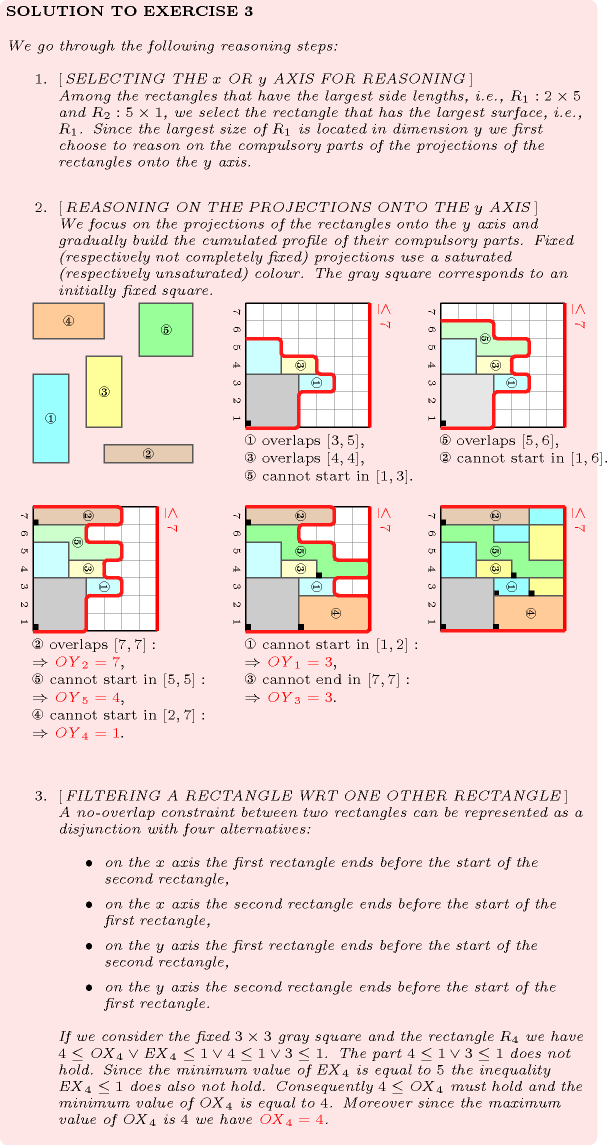
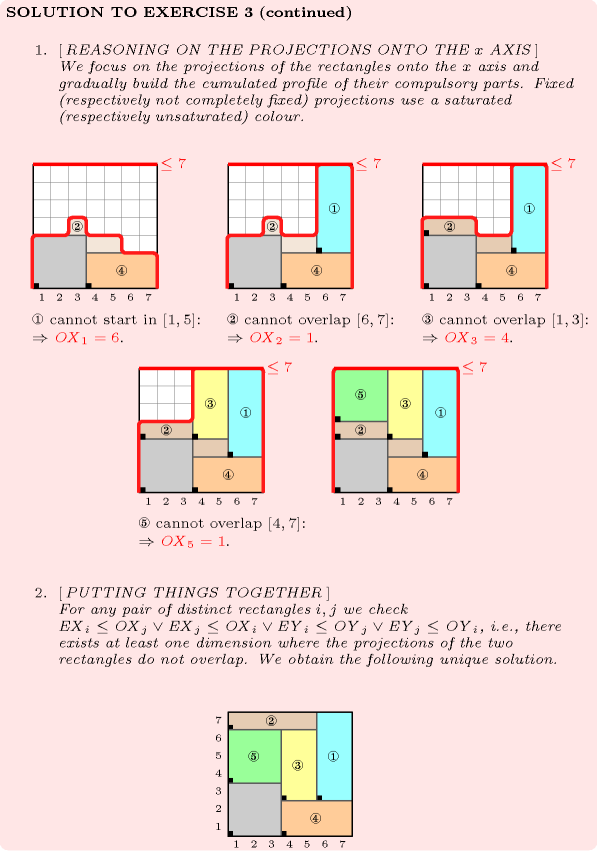
- Quiz
: checking whether a ground instance holds or not

: finding all solutions

: finding the unique solution

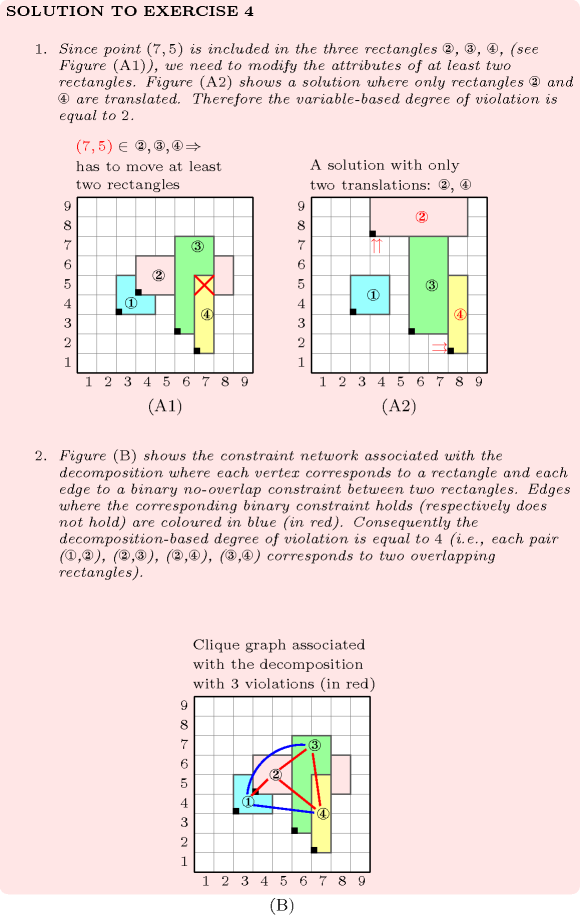
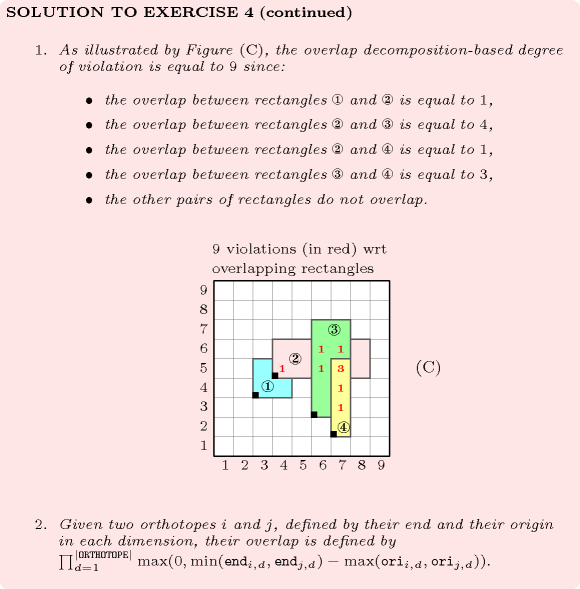
: degrees of violation for non-overlapping