5.131. distance_change
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
is equal to the number of times one of the following two conditions is true :
holds and does not hold,
holds and does not hold.
- Example
-
The constraint holds since the following condition () is verified: .
- Typical
- Symmetries
Arguments are permutable w.r.t. permutation .
One and the same constant can be added to the attribute of all items of .
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by , and .
- Usage
Measure the distance between two sequences according to the constraint.
- Remark
We measure that distance with respect to a given constraint and not according to the fact that the variables are assigned distinct values.
- See also
- Keywords
characteristic of a constraint: automaton, automaton with counters.
constraint arguments: pure functional dependency.
constraint network structure: sliding cyclic(2) constraint network(2).
- Arc input(s)
/
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Within the Arc input(s) slot, the character / indicates that we generate two distinct graphs. The graph property measures the distance between two digraphs and . This distance is defined as the sum of the following quantities:
The number of arcs of that do not belong to ,
The number of arcs of that do not belong to .
Part (A) of Figure 5.131.1 gives the final graph associated with the sequence -3,-3,-1,-2,-2 (i.e., the second argument of the constraint of the Example slot), while part (B) shows the final graph corresponding to -4,-4,-3,-3,-3 (i.e., the third argument of the constraint of the Example slot). Since arc belongs to the first final graph but not to the second one, the distance between the two final graphs is equal to 1.
Figure 5.131.1. Final graphs of the constraint
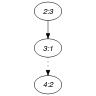
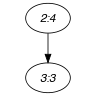
(a) (b)
- Automaton
Figure 5.131.2 depicts the automaton associated with the constraint. Let and respectively be the pairs of consecutive variables of the collections and . To each quadruple corresponds a 0-1 signature variable . The following signature constraint links these variables:
.
Figure 5.131.2. Automaton of the constraint
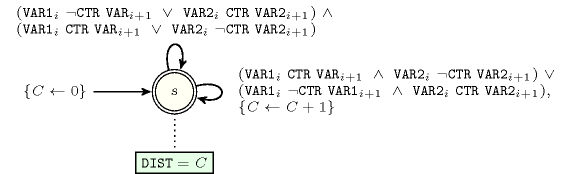
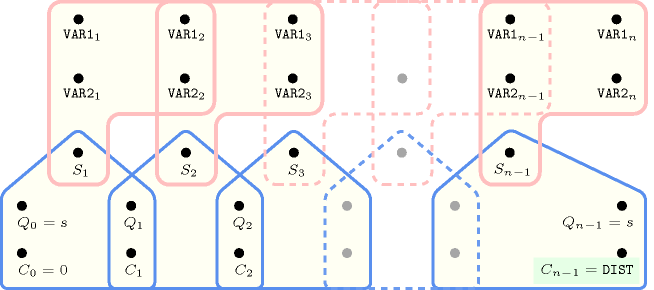
Figure 5.131.3. Hypergraph of the reformulation corresponding to the automaton of the constraint