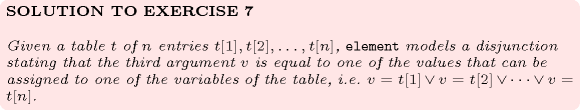5.139. element
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Synonyms
, , .
- Arguments
- Restrictions
- Purpose
is equal to the item of , i.e. .
- Example
-
The constraint holds since its third argument is equal to the 3th () item of the collection .
- All solutions
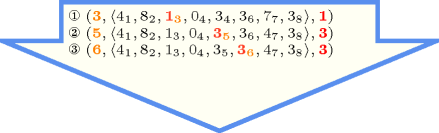
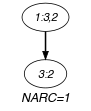
Figure 5.139.1 gives all solutions to the following non ground instance of the constraint: , , .
Figure 5.139.1. All solutions corresponding to the non ground example of the constraint of the All solutions slot
- Typical
- Symmetry
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Arg. properties
Functional dependency: determined by and .
Suffix-extensible wrt. .
- Usage
- Remark
In the original constraint of CHIP the attribute was not explicitly present in the table of values. It was implicitly defined as the position of a value in the previous table.
Within some systems (e.g., Gecode), the index of the first entry of the table corresponds to 0 rather than to 1.
When the first entry of the table corresponds to a value that is different from 1 we can still use the constraint. We use the reformulation , where and are domain variables respectively ranging from 1 to and from to .
The constraint is called in Choco (http://choco.sourceforge.net/). It is also sometimes called when the second argument corresponds to a table of variables.
The constraint [Sicstus95] is a generalisation of the constraint, where the table is replaced by a directed acyclic graph describing the set of solutions: there is a one to one correspondence between the solutions and the paths from the unique source of the dag to its leaves.
- Systems
nth in Choco, element in Gecode, element in JaCoP, element in MiniZinc, element in SICStus.
- See also
common keyword: , , , , , (array constraint), , , , , (data constraint).
generalisation: ( replaced by of ).
implies: .
related: ((pairs linked by an element with the same table)).
uses in its reformulation: , , , , .
- Keywords
characteristic of a constraint: core, automaton, automaton without counters, reified automaton constraint, derived collection.
constraint arguments: pure functional dependency.
constraint network structure: centered cyclic(2) constraint network(1).
constraint type: data constraint.
heuristics: labelling by increasing cost, regret based heuristics.
modelling: array constraint, table, functional dependency, variable indexing, variable subscript, disjunction, assignment to the same set of values, sequence dependent set-up.
modelling exercises: assignment to the same set of values, sequence dependent set-up, zebra puzzle.
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
The original constraint with three arguments. We use the derived collection for putting together the and parameters of the constraint. Within the arc constraint we use the implicit attribute that associates to each item of a collection its position within the collection.
Parts (A) and (B) of Figure 5.139.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold.
Figure 5.139.2. Initial and final graph of the constraint
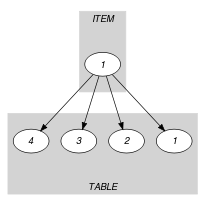
(a) (b) - Signature
Because of the first condition of the arc constraint the final graph cannot have more than one arc. Therefore we can rewrite to and simplify to .
- Automaton
Figure 5.139.3 depicts the automaton associated with the constraint. Let be the attribute of item of the collection. To each triple corresponds a 0-1 signature variable as well as the following signature constraint: .
Figure 5.139.3. Automaton of the constraint (once one finds the right index and value in the table, one switches from the initial state to the accepting state )
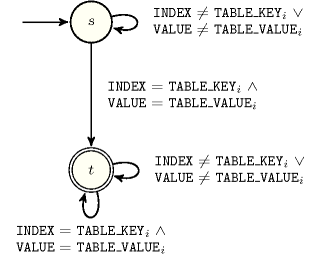
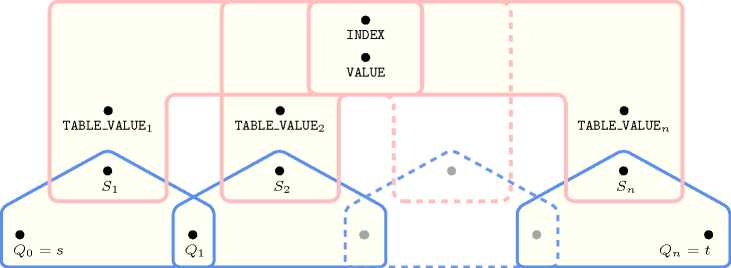
Figure 5.139.4. Hypergraph of the reformulation corresponding to the automaton of the constraint
- Quiz
: checking whether a ground instance holds or not

: finding all solutions

: finding all solutions

: identifying infeasible values

: variable-based degree of violation

: using entailment for counting

: modelling with an unconstrained index

: modelling an index starting at 0

: modelling indirection