5.143. element_product
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
is equal to the item of multiplied by .
- Example
-
The constraint holds since its fourth argument is equal to the 3th () item of the collection multiplied by .
- Typical
- Arg. properties
Functional dependency: determined by , and .
Suffix-extensible wrt. .
- Usage
The constraint was originally used in configuration problems [OttossonThorsteinsson00]. In this context, denotes the cost of buying units of type at cost .
- Reformulation
By introducing an extra variable , the constraint can be expressed in term of an constraint and of a product constraint .
- See also
common keyword: , , , (array constraint).
- Keywords
application area: configuration problem.
constraint arguments: pure functional dependency.
constraint type: data constraint.
modelling: array constraint, table, functional dependency, variable subscript.
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
We use the derived collection for putting together the , the and parameters of the constraint. Within the arc constraint we use the implicit attribute that associates to each item of a collection its position within the collection.
Parts (A) and (B) of Figure 5.143.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold.
Figure 5.143.1. Initial and final graph of the constraint
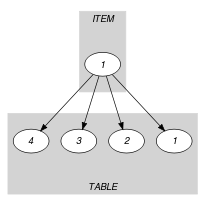
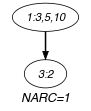
(a) (b) - Signature
Because of the first condition of the arc constraint the final graph cannot have more than one arc. Therefore we can rewrite to and simplify to .