5.169. golomb
| DESCRIPTION | LINKS | GRAPH |
- Origin
Inspired by [Golomb72].
- Constraint
- Argument
- Restrictions
- Purpose
Given a strictly increasing sequence , enforce all differences between two variables and to be distinct.
- Example
-
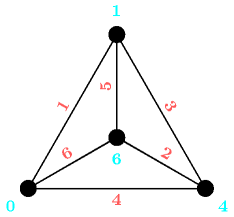
Figure 5.169.1 gives a graphical interpretation of the solution given in the example in term of a graph: each vertex corresponds to a value of , while each arc depicts a difference between two values. The constraint holds since one can note that these differences 1, 4, 6, 3, 5, 2 are all-distinct.
Figure 5.169.1. Graphical representation of the solution , , , (differences are displayed in light red and are pairwise distinct).
- Typical
- Symmetry
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Contractible wrt. .
- Usage
This constraint refers to the Golomb ruler problem. We quote the definition from [Shearer96]: “A Golomb ruler is a set of integers (marks) such that all the differences are distinct”.
- Remark
Different constraints models for the Golomb ruler problem were presented in [SmithStergiouWalsh99].
- Algorithm
At a first glance, one could think that, because it looks so similar to the constraint, we could have a perfect polynomial filtering algorithm. However this is not true since one retrieves the same variable in different vertices of the graph. This leads to the fact that one has incompatible arcs in the bipartite graph (the two classes of vertices correspond to the pair of variables and to the fact that the difference between two pairs of variables takes a specific value). However one can still reuse a similar filtering algorithm as for the constraint, but this will not lead to perfect pruning.
- Counting
-
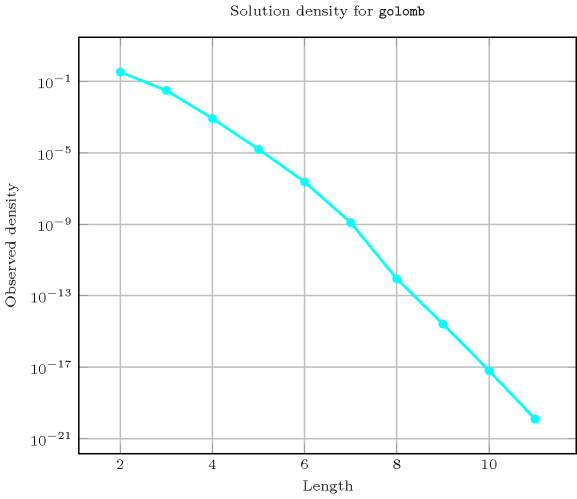
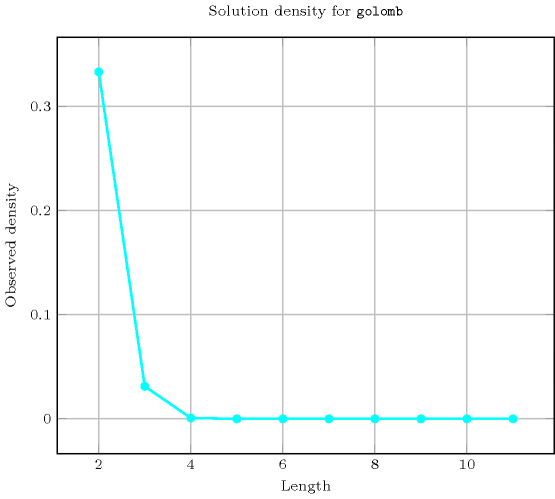
Length () 2 3 4 5 6 7 8 9 10 11 Solutions 3 2 2 4 8 10 2 2 2 4 Number of solutions for : domains
- See also
common keyword: (all different).
implies: .
- Keywords
characteristic of a constraint: disequality, difference, all different, derived collection.
- Cond. implications
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
When applied on the collection of items , the generator of derived collection generates the following collection of items: . Note that we use a binary arc constraint between two vertices and that this binary constraint involves four variables.
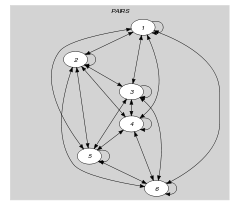
Parts (A) and (B) of Figure 5.169.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property we show one of the largest strongly connected components of the final graph. The constraint holds since all the strongly connected components have at most one vertex: the differences 1, 2, 3, 4, 5, 6 that one can construct from the values 0, 1, 4, 6 assigned to the variables of the collection are all-distinct.
Figure 5.169.2. Initial and final graph of the constraint
(a) 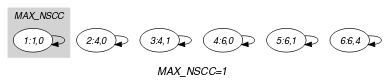
(b)