Global Constraint Catalog: Cin

5.181. in_relation

DESCRIPTION

LINKS

GRAPH

Origin

Constraint explicitly defined by tuples of values.

Constraint

$𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂)$

Synonyms

$𝚌𝚊𝚜𝚎$ , $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗$ , $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗𝚊𝚕$ , $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗𝚊𝚕_𝚜𝚞𝚙𝚙𝚘𝚛𝚝$ , $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗𝚊𝚕_𝚜𝚞𝚙𝚙𝚘𝚛𝚝𝚟𝚊$ , $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗𝚊𝚕_𝚜𝚞𝚙𝚙𝚘𝚛𝚝𝚖𝚍𝚍$ , $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗𝚊𝚕_𝚜𝚞𝚙𝚙𝚘𝚛𝚝𝚜𝚝𝚛$ , $𝚏𝚎𝚊𝚜𝚝𝚞𝚙𝚕𝚎𝚊𝚌$ , $𝚝𝚊𝚋𝚕𝚎$ .

Types

$𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝚁𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝙻𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝚁𝚂$
$𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚞𝚙𝚕𝚎 - 𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝙻𝚂)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝚁𝚂, 𝚟𝚊𝚛)

| 𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝚁𝚂 | \geq 1

| 𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝙻𝚂 | \geq 1

| 𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝙻𝚂 | = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝙻𝚂, 𝚟𝚊𝚕)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂, 𝚝𝚞𝚙𝚕𝚎)

Purpose

Enforce the tuple of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to take its value out of a set of tuples of values $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂$ . The value of a tuple of variables $〈 V_{1}, V_{2}, \dots, V_{n} 〉$ is a tuple of values $〈 U_{1}, U_{2}, \dots, U_{n} 〉$ if and only if $V_{1} = U_{1} \land V_{2} = U_{2} \land \dots \land V_{n} = U_{n}$ .

Example

(\begin{matrix} 〈5, 3, 3〉, \\ 〈𝚝𝚞𝚙𝚕𝚎 - 〈5, 2, 3〉, 𝚝𝚞𝚙𝚕𝚎 - 〈5, 2, 6〉, 𝚝𝚞𝚙𝚕𝚎 - 〈5, 3, 3〉〉 \end{matrix})

The $𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗$ constraint holds since its first argument $〈 5, 3, 3 〉$ corresponds to the third item of the collection of tuples $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂$ .

Typical

| 𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝚁𝚂 | > 1

Symmetries

Items of $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂 . 𝚝𝚞𝚙𝚕𝚎$ are permutable (same permutation used).
All occurrences of two distinct tuples of values in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ or $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂 . 𝚝𝚞𝚙𝚕𝚎$ can be swapped; all occurrences of a tuple of values in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ or $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂 . 𝚝𝚞𝚙𝚕𝚎$ can be renamed to any unused tuple of values.

Arg. properties

Extensible wrt. $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂$ .

Usage

Quite often some constraints cannot be easily expressed, neither by a formula, nor by a regular pattern. In this case one has to define the constraint by specifying in extension the combinations of allowed values.

Remark

The $𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗$ constraint is called $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗𝚊𝚕_𝚜𝚞𝚙𝚙𝚘𝚛𝚝$ in JaCoP (http://www.jacop.eu/). Within SICStus Prolog the constraint can be applied to more than a single tuple of variables and is called $𝚝𝚊𝚋𝚕𝚎$ . Within [BourdaisGalinierPesant03] this constraint is called $𝚎𝚡𝚝𝚎𝚗𝚜𝚒𝚘𝚗$ .

The $𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗$ constraint is called $𝚝𝚊𝚋𝚕𝚎$ in MiniZinc (http://www.minizinc.org/).

Systems

feasPairAC in Choco, infeasPairAC in Choco, relationPairAC in Choco, feasTupleAC in Choco, infeasTupleAC in Choco, relationTupleAC in Choco, extensional in Gecode, extensionalsupportVA in JaCoP, extensionalsupportMDD in JaCoP, extensionalsupportSTR in JaCoP, table in MiniZinc, case in SICStus, relation in SICStus, table in SICStus.

Used in

$𝚌𝚘𝚗𝚍_𝚕𝚎𝚡_𝚌𝚘𝚜𝚝$ , $𝚌𝚘𝚗𝚍_𝚕𝚎𝚡_𝚐𝚛𝚎𝚊𝚝𝚎𝚛$ , $𝚌𝚘𝚗𝚍_𝚕𝚎𝚡_𝚐𝚛𝚎𝚊𝚝𝚎𝚛𝚎𝚚$ , $𝚌𝚘𝚗𝚍_𝚕𝚎𝚡_𝚕𝚎𝚜𝚜$ , $𝚌𝚘𝚗𝚍_𝚕𝚎𝚡_𝚕𝚎𝚜𝚜𝚎𝚚$ .

cost variant: $𝚌𝚘𝚗𝚍_𝚕𝚎𝚡_𝚌𝚘𝚜𝚝$ ( $𝙲𝙾𝚂𝚃$ parameter added).

used in graph description: $𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎$ .

Keywords

characteristic of a constraint: tuple, derived collection.

combinatorial object: relation.

constraint type: data constraint, extension.

filtering: arc-consistency.

Derived Collection

𝚌𝚘𝚕 (\begin{matrix} 𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝚁𝚂 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌 - 𝚃𝚄𝙿𝙻𝙴_𝙾𝙵_𝚅𝙰𝚁𝚂), \\ 𝚒𝚝𝚎𝚖 (𝚟𝚎𝚌 - 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)] \end{matrix})

Arc input(s)

$𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝚁𝚂$ $𝚃𝚄𝙿𝙻𝙴𝚂_𝙾𝙵_𝚅𝙰𝙻𝚂$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚞𝚙𝚕𝚎𝚜_𝚘𝚏_𝚟𝚊𝚛𝚜, 𝚝𝚞𝚙𝚕𝚎𝚜_𝚘𝚏_𝚟𝚊𝚕𝚜)

Arc arity

Arc constraint(s)

𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎

(𝚝𝚞𝚙𝚕𝚎𝚜_𝚘𝚏_𝚟𝚊𝚛𝚜 . 𝚟𝚎𝚌, 𝚝𝚞𝚙𝚕𝚎𝚜_𝚘𝚏_𝚟𝚊𝚕𝚜 . 𝚝𝚞𝚙𝚕𝚎)

Graph property(ies)

𝐍𝐀𝐑𝐂

\geq 1

Graph model

Parts (A) and (B) of Figure 5.181.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the unique arc of the final graph is stressed in bold.

Figure 5.181.1. Initial and final graph of the $𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗$ constraint


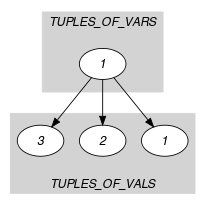
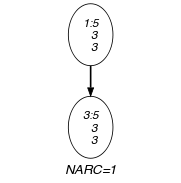
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.181. in_relation

Figure 5.181.1. Initial and final graph of the 𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗 constraint

Figure 5.181.1. Initial and final graph of the $𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗$ constraint