5.182. in_same_partition
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
Used for defining several entries of this catalog.
- Constraint
- Type
- Arguments
- Restrictions
- Purpose
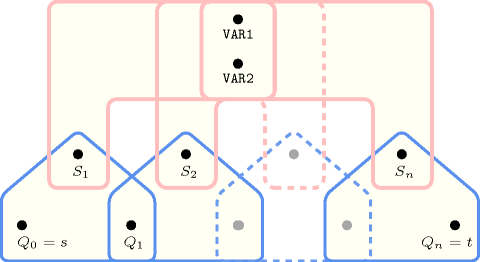
Enforce and to be respectively assigned to values and that both belong to a same partition of the collection .
- Example
-
The constraint holds since its first and second arguments and both belong to the third partition of its third argument .
- Typical
- Symmetries
Arguments are permutable w.r.t. permutation .
Items of are permutable.
Items of are permutable.
- Arg. properties
Extensible wrt. .
- Used in
- See also
- Keywords
characteristic of a constraint: partition, automaton, automaton without counters, reified automaton constraint, derived collection.
constraint arguments: binary constraint.
constraint network structure: centered cyclic(2) constraint network(1).
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
and are put together in the derived collection . Since both and should take their value in one of the partition depicted by the collection, the final graph should have two sources corresponding respectively to and . Since two, possibly distinct, values should be assigned to and and since these values belong to the same partition the final graph should only have one sink. This sink corresponds in fact to partition .
Parts (A) and (B) of Figure 5.182.1 respectively show the initial and final graph associated with the Example slot. Since we both use the and graph properties, the source and sink vertices of the final graph are shown with a double circle.
Figure 5.182.1. Initial and final graph of the constraint
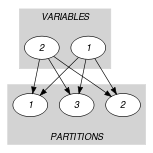
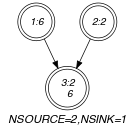
(a) (b) - Signature
Note that the sinks of the initial graph cannot become sources of the final graph since isolated vertices are eliminated from the final graph. Since the final graph contains two sources it also includes one arc between a source and a sink. Therefore the minimum number of sinks of the final graph is equal to one. So we can rewrite to and simplify to .
- Automaton
Figure 5.182.2 depicts the automaton associated with the constraint. Let be the attribute of the item of the collection. To each triple corresponds a 0-1 signature variable as well as the following signature constraint: .
Figure 5.182.2. Automaton of the constraint
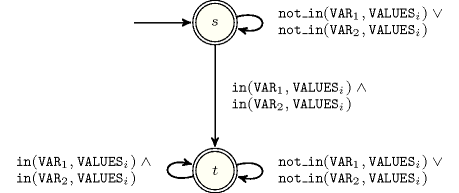
Figure 5.182.3. Hypergraph of the reformulation corresponding to the automaton of the constraint