5.187. increasing_nvalue
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
The variables of the collection are increasing. In addition, is the number of distinct values taken by the variables of the collection .
- Example
-
The first constraint (see Figure 5.187.1 for a graphical representation) holds since:
The values of the collection are sorted in increasing order.
is set to the number of distinct values occurring within the collection .
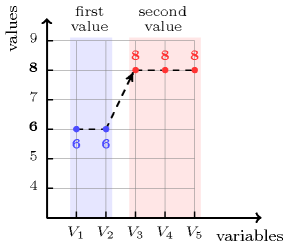
Figure 5.187.1. Illustration of the first example of the Example slot: five variables , , , , respectively fixed to values 6, 6, 8, 8 and 8, and the corresponding number of distinct values
- Typical
- Symmetry
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by .
- Algorithm
A complete filtering algorithm in a linear time complexity over the sum of the domain sizes is described in [BeldiceanuHermenierLorcaPetit10].
- Reformulation
The constraint can be expressed in term of a conjunction of a and an constraints (i.e., a chain of non strict inequality constraints on adjacent variables of the collection ). But as shown by the following example, , , , (), this hinders propagation (i.e., the unique solution , is not directly obtained after stating all the previous constraints).
A better reformulation achieving arc-consistency uses the constraint [PetitBeldiceanuLorca11] that we now introduce. Given a domain variable, a sequence of domain variables, and and two binary constraints, holds if (1) is equal to the number of -stretches in the sequence , and (2) holds on any pair of consecutive variables in . A -stretch is a generalisation of the notion of stretch introduced by G. Pesant [Pesant01], where the equality constraint is made explicit by replacing it by a binary constraint , i.e., a -stretch is a maximal length subsequence of for which the binary constraint is satisfied on consecutive variables. can be reformulated as .
- Counting
-
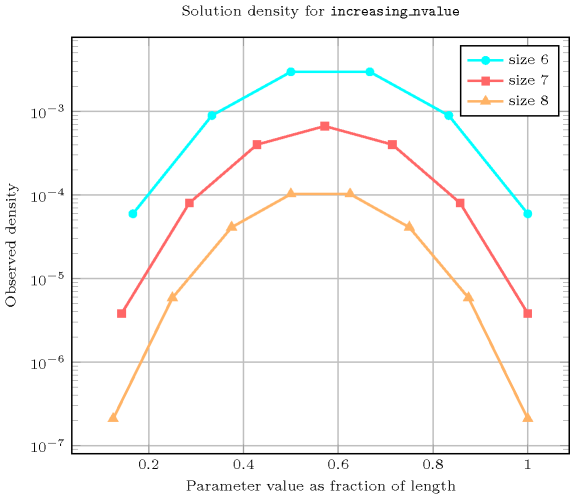
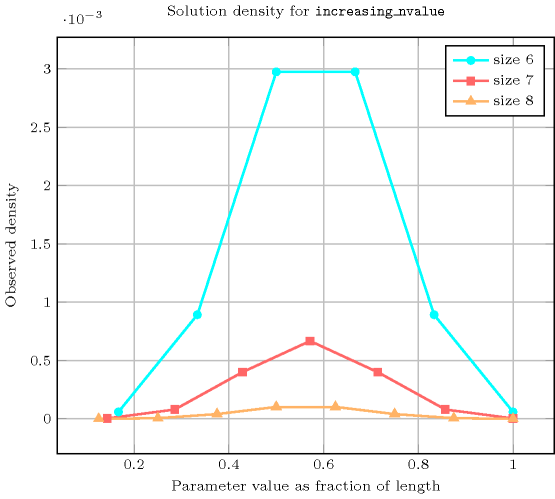
Length () 2 3 4 5 6 7 8 Solutions 6 20 70 252 924 3432 12870 Number of solutions for : domains
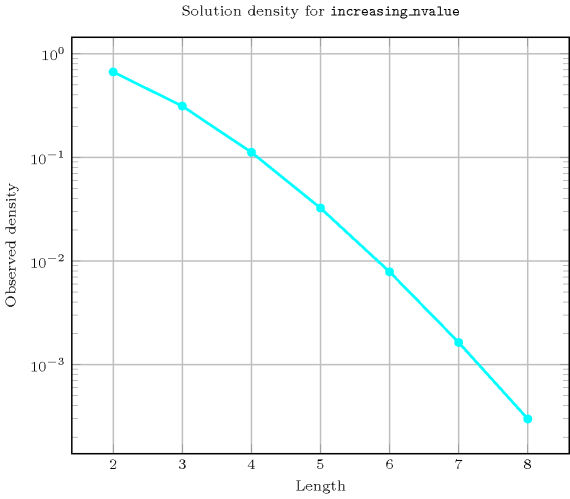
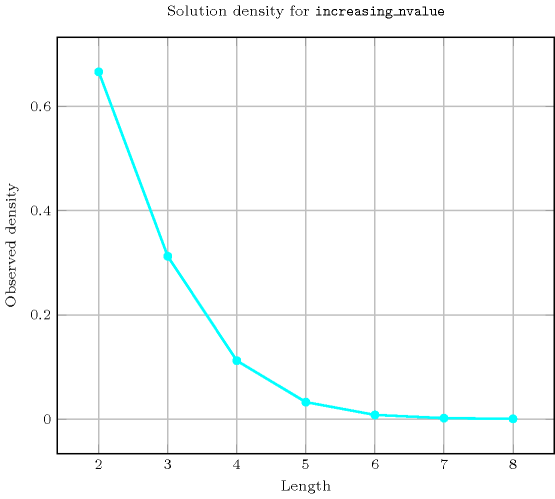
Length () 2 3 4 5 6 7 8 Total 6 20 70 252 924 3432 12870 Parameter value 1 3 4 5 6 7 8 9 2 3 12 30 60 105 168 252 3 - 4 30 120 350 840 1764 4 - - 5 60 350 1400 4410 5 - - - 6 105 840 4410 6 - - - - 7 168 1764 7 - - - - - 8 252 8 - - - - - - 9 Solution count for : domains
- Systems
- See also
implies: (remove parameter from ), , .
related: .
shift of concept: ( replaced by and replaced by ).
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint network structure: Berge-acyclic constraint network.
constraint type: counting constraint, value partitioning constraint, order constraint.
final graph structure: strongly connected component, equivalence.
modelling: number of distinct equivalence classes, number of distinct values, functional dependency.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
Parts (A) and (B) of Figure 5.187.2 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property we show the different strongly connected components of the final graph. Each strongly connected component corresponds to a value that is assigned to some variables of the collection. The 2 following values 6 and 8 are used by the variables of the collection.
Figure 5.187.2. Initial and final graph of the constraint
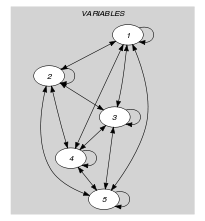
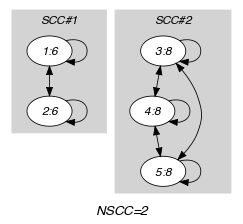
(a) (b)
- Automaton
A first systematic approach for creating an automaton that only recognises the solutions to the constraint could be to:
First, create an automaton that recognises the solutions to the constraint.
Second, create an automaton that recognises the solutions to the constraint.
Third, make the product of the two previous automata and minimise the resulting automaton.
However this approach is not going to scale well in practice since the automaton associated with the constraint has a too big size. Therefore we propose an approach where we directly construct in a single step the automaton that only recognises the solutions to the constraint. Note that we do not have any formal proof that the resulting automaton is always minimum.
Without loss of generality, assume that the collection of variables contains at least one variable (i.e., ). Let , , , and respectively denote the minimum and maximum possible value of variable , the number of variables of the collection , the smallest value that can be assigned to the variables of , and the largest value that can be assigned to the variables of . Let denote the total number of potential values. Clearly, the maximum number of distinct values that can be assigned to the variables of the collection cannot exceed the quantity . The states of the automaton that only accepts solutions to the constraint can be defined in the following way:
We have an initial state labelled by .
We have states labelled by . The first index of a state corresponds to the number of distinct values already encountered, while the second index denotes the the current value (i.e., more precisely the index of the current value, where the minimum value has index 1).
Terminal states depend on the possible values of variable and correspond to those states such that is a possible value for variable . Note that we assume no further restriction on the domain of (otherwise the set of accepting states needs to be reduced in order to reflect the current set of possible values of ). Three classes of transitions are respectively defined in the following way:
There is a transition, labelled by , from the initial state to the state .
There is a loop, labelled by for every state .
there is a transition labelled by from to .
We respectively have transitions of class 1, transitions of class 2, and transitions of class 3.
Note that all states such that can be discarded since they do not allow to reach the minimum number of distinct values required .
Part (A) of Figure 5.187.3 depicts the automaton associated with the constraint of the first example of the Example slot. For this purpose, we assume that variable is fixed to value 2 and that variables of the collection take their values within interval . Part (B) of Figure 5.187.3 represents the simplified automaton where all states that do not allow to reach an accepting state were removed. The corresponding constraint holds since the corresponding sequence of visited states, , ends up in an accepting state (i.e., accepting states are denoted graphically by a double circle).
Figure 5.187.3. Automaton – Part (A) – and simplified automaton – Part (B) – of the constraint of the first example of the Example slot: the path corresponding to the second argument is depicted by thick orange arcs, where the self-loop on state is applied twice
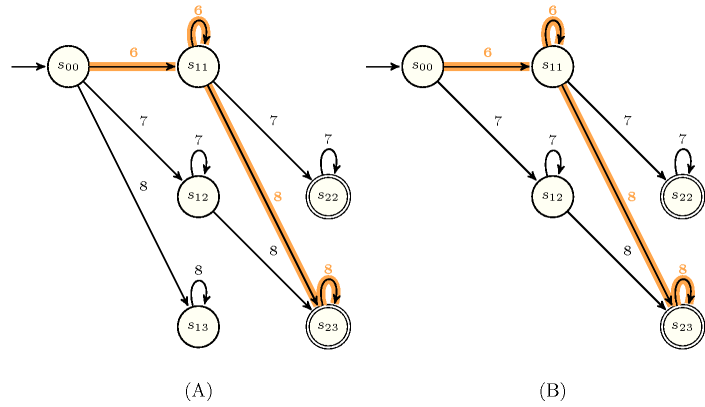
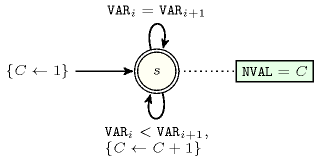
Figure 5.187.4 depicts a second deterministic automaton with one counter associated with the constraint, where the argument is unified to the final value of the counter.
Figure 5.187.4. Automaton (with one counter) of the constraint for a non-empty collection of variables