Global Constraint Catalog: Cinterval_and

5.198. interval_and_sum

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ .

Constraint

$𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖 (𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻, 𝚃𝙰𝚂𝙺𝚂, 𝙻𝙸𝙼𝙸𝚃)$

Arguments

$𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$	$𝚒𝚗𝚝$
$𝚃𝙰𝚂𝙺𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚍𝚟𝚊𝚛, 𝚑𝚎𝚒𝚐𝚑𝚝 - 𝚍𝚟𝚊𝚛)$
$𝙻𝙸𝙼𝙸𝚃$	$𝚒𝚗𝚝$

Restrictions

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝚂𝙺𝚂, [𝚘𝚛𝚒𝚐𝚒𝚗, 𝚑𝚎𝚒𝚐𝚑𝚝])

𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗 \geq 0

𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝 \geq 0

𝙻𝙸𝙼𝙸𝚃 \geq 0

Purpose

A maximum resource capacity constraint: We have to fix the origins of a collection of tasks in such a way that, for all the tasks that are allocated to the same interval, the sum of the heights does not exceed a given capacity. All the intervals we consider have the following form: $[k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻, k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ , where $k$ is an integer.

Example

(\begin{matrix} 5, 〈\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 1 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 10 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 10 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 3, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 4 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 1 \end{matrix}〉, 5 \end{matrix})

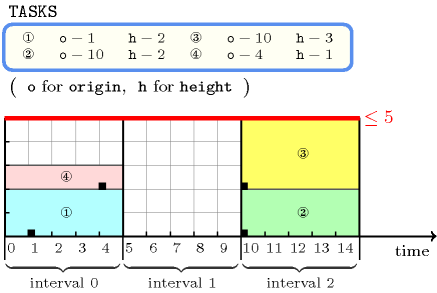
Figure 5.198.1 shows the solution associated with the example. The constraint $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ holds since the sum of the heights of the tasks that are located in the same interval does not exceed the limit 5. Each task $t$ is depicted by a rectangle $r$ associated with the interval to which the task $t$ is assigned. The rectangle $r$ is labelled with the position of $t$ within the items of the $𝚃𝙰𝚂𝙺𝚂$ collection. The origin of task $t$ is represented by a small black square located within its corresponding rectangle $r$ . Finally, the height of a rectangle $r$ is equal to the height of the task $t$ to which it corresponds.

Figure 5.198.1. The $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ solution to the Example slot with the use of each interval

Typical

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 1

| 𝚃𝙰𝚂𝙺𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝) > 1

𝙻𝙸𝙼𝙸𝚃 <

𝚜𝚞𝚖

(𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝)

Symmetries

Items of $𝚃𝙰𝚂𝙺𝚂$ are permutable.
One and the same constant can be added to the $𝚘𝚛𝚒𝚐𝚒𝚗$ attribute of all items of $𝚃𝙰𝚂𝙺𝚂$ .
An occurrence of a value of $𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗$ that belongs to the $k$ -th interval, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be replaced by any other value of the same interval.
$𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝$ can be decreased to any value $\geq 0$ .
$𝙻𝙸𝙼𝙸𝚃$ can be increased.

Arg. properties

Contractible wrt. $𝚃𝙰𝚂𝙺𝚂$ .

Usage

This constraint can be use for timetabling problems. In this context the different intervals are interpreted as morning and afternoon periods of different consecutive days. We have a capacity constraint for all tasks that are assigned to the same morning or afternoon of a given day.

Reformulation

Let $K$ denote the index of the last possible interval where the tasks can be assigned: $K = ⌊ \frac{{max}_{i \in [1, | 𝚃𝙰𝚂𝙺𝚂 |]} (\bar{𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗}) + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1}{𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻} ⌋$ . The $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ $(𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻, 𝚃𝙰𝚂𝙺𝚂, 𝙻𝙸𝙼𝙸𝚃)$ constraint can be expressed in term of a set of reified constraints and of $K$ arithmetic constraints (i.e., $𝚜𝚌𝚊𝚕𝚊𝚛_𝚙𝚛𝚘𝚍𝚞𝚌𝚝$ constraints).

For each task $𝚃𝙰𝚂𝙺𝚂 [i]$ $(i \in [1, | 𝚃𝙰𝚂𝙺𝚂 |])$ and for each interval $[k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻, k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ $(k \in [0, K])$ we create a 0-1 variable $B_{i k}$ that will be set to 1 if and only if the origin of task $𝚃𝙰𝚂𝙺𝚂 [i]$ is assigned within interval $[k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻, k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ :

$B_{i k} \Leftrightarrow 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 \geq k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \land$

$𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1$
Finally, for each interval $[k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻, k \cdot 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ $(k \in [0, K])$ , we impose the sum $𝚃𝙰𝚂𝙺𝚂 [1] . 𝚑𝚎𝚒𝚐𝚑𝚝 \cdot B_{1 k} + 𝚃𝙰𝚂𝙺𝚂 [2] . 𝚑𝚎𝚒𝚐𝚑𝚝 \cdot B_{2 k} + \dots + 𝚃𝙰𝚂𝙺𝚂 [| 𝚃𝙰𝚂𝙺𝚂 |] . 𝚑𝚎𝚒𝚐𝚑𝚝 \cdot B_{| 𝚃𝙰𝚂𝙺𝚂 | k}$ to not exceed the maximum allowed capacity $𝙻𝙸𝙼𝙸𝚃$ .

See also

assignment dimension removed: $𝚜𝚞𝚖_𝚌𝚝𝚛$ (assignment dimension corresponding to intervals is removed).

used in graph description: $𝚜𝚞𝚖_𝚌𝚝𝚛$ .

Keywords

application area: assignment.

characteristic of a constraint: automaton, automaton with array of counters.

constraint type: timetabling constraint, resource constraint, temporal constraint.

modelling: assignment dimension, interval.

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$ $𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜 1, 𝚝𝚊𝚜𝚔𝚜 2)

Arc arity

Arc constraint(s)

𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻

Sets

\begin{matrix} 𝖲𝖴𝖢𝖢 \mapsto \\ [\begin{matrix} 𝚜𝚘𝚞𝚛𝚌𝚎, \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 - 𝚌𝚘𝚕 (\begin{matrix} 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛), \\ 𝚒𝚝𝚎𝚖 (𝚟𝚊𝚛 - 𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝)] \end{matrix}) \end{matrix}] \end{matrix}

Constraint(s) on sets

𝚜𝚞𝚖_𝚌𝚝𝚛

(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, \leq, 𝙻𝙸𝙼𝙸𝚃)

Graph model

We use a bipartite graph where each class of vertices corresponds to the different tasks of the $𝚃𝙰𝚂𝙺𝚂$ collection. There is an arc between two tasks if their origins belong to the same interval. Finally we enforce a $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraint on each set $𝒮$ of successors of the different vertices of the final graph. This put a restriction on the maximum value of the sum of the $𝚑𝚎𝚒𝚐𝚑𝚝$ attributes of the tasks of $𝒮$ .

Parts (A) and (B) of Figure 5.198.2 respectively show the initial and final graph associated with the Example slot. Each connected component of the final graph corresponds to items that are all assigned to the same interval.

Figure 5.198.2. Initial and final graph of the $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ constraint


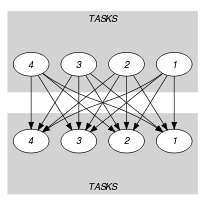
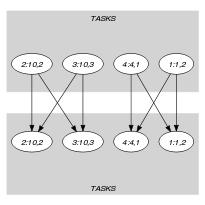
(a)	(b)

Automaton: Figure 5.198.3 depicts the automaton associated with the $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ constraint. To each item of the collection $𝚃𝙰𝚂𝙺𝚂$ corresponds a signature variable $S_{i}$ that is equal to 1.

Figure 5.198.3. Automaton of the $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.198. interval_and_sum

Figure 5.198.1. The $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ solution to the Example slot with the use of each interval

Figure 5.198.2. Initial and final graph of the $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ constraint

Figure 5.198.3. Automaton of the $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.198. interval_and_sum

Figure 5.198.1. The 𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖 solution to the Example slot with the use of each interval

Figure 5.198.2. Initial and final graph of the 𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖 constraint

Figure 5.198.3. Automaton of the 𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖 constraint

Figure 5.198.1. The $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ solution to the Example slot with the use of each interval

Figure 5.198.2. Initial and final graph of the $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ constraint

Figure 5.198.3. Automaton of the $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ constraint