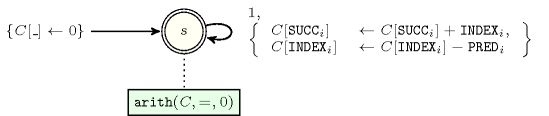5.199. inverse
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
CHIP
- Constraint
- Synonyms
, , .
- Argument
- Restrictions
- Purpose
Enforce each vertex of a digraph to have exactly one predecessor and one successor. In addition the following two statements are equivalent:
The successor of the node is the node.
The predecessor of the node is the node.
- Example
-
The constraint holds since:
,
,
,
,
.
- Typical
- Symmetries
Items of are permutable.
Attributes of are permutable w.r.t. permutation (permutation applied to all items).
- Arg. properties
Functional dependency: determined by and .
Functional dependency: determined by and .
- Usage
This constraint is used in order to make the link between the successor and the predecessor variables. This is sometimes required by specific heuristics that use both predecessor and successor variables. In some problems, the and variables are respectively interpreted as column an row variables (i.e., we have a bijection between the variables and their values). This is for instance the case in the -queens problem (i.e., place queens on an by chessboard in such a way that no two queens are on the same row, the same column or the same diagonal) when we use the following model: to each column of the chessboard we associate a variable that gives the row where the corresponding queen is located. Symmetrically, to each row of the chessboard we create a variable that indicates the column where the associated queen is placed. Having these two sets of variables, we can now write a heuristics that selects the column or the row for which we have the fewest number of alternatives for placing a queen.
- Remark
In the original constraint of CHIP the attribute was not explicitly present. It was implicitly defined as the position of a variable in a list, the first position being 1. This is also the case for SICStus Prolog, JaCoP and Gecode where the variables are respectively indexed from 1, 0 and 0. Within SICStus Prolog and JaCoP (http://www.jacop.eu/), the constraint is called . Within Gecode, it is called (http://www.gecode.org/).
- Algorithm
An arc-consistency filtering algorithm for the constraint is described in [Cymer12], [CymerPhD13]. The algorithm is based on the following ideas:
We first normalize the domains of the variables by removing value from the variable if value does not belong to the variable, and by removing value from the variable if value does not belong to the variable.
Second, one can map solutions to the constraint to perfect matchings in a so-called variable bipartite graph derived from the domain of the variables of the constraint in the following way: to each successor variable corresponds a vertex; similarly to each predecessor variable corresponds a vertex; there is and edge between the variable and the variable if and only if value belongs to the domain of the variable and value belongs to the domain of the variable.
Third, Dulmage-Mendelsohn decomposition [DulmageMendelsohn58] is used to characterise all edges that do not belong to any perfect matching, and therefore prune the corresponding variables.
- Systems
inverseChanneling in Choco, channel in Gecode, inverse in MiniZinc, assignment in SICStus.
- See also
common keyword: , (permutation).
generalisation: (do not assume anymore that the smallest value of the or attributes is equal to 1), ( replaced by ), (partial mapping between two collections of distinct size).
- Keywords
characteristic of a constraint: automaton, automaton with array of counters.
combinatorial object: permutation.
constraint arguments: pure functional dependency.
constraint type: graph constraint.
filtering: bipartite matching, arc-consistency.
modelling: channelling constraint, permutation channel, dual model, functional dependency.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
In order to express the binary constraint that links two vertices one has to make explicit the identifier of the vertices. This is why the constraint considers objects that have three attributes:
One fixed attribute that is the identifier of the vertex,
One variable attribute that is the successor of the vertex,
One variable attribute that is the predecessor of the vertex.
Parts (A) and (B) of Figure 5.199.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold.
Figure 5.199.1. Initial and final graph of the constraint
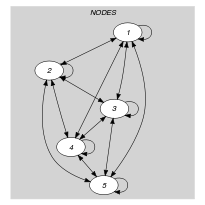
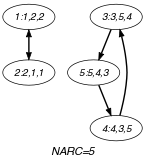
(a) (b) - Signature
Since all the attributes of the collection are distinct and because of the first condition of the arc constraint all the vertices of the final graph have at most one predecessor.
Since all the attributes of the collection are distinct and because of the second condition of the arc constraint all the vertices of the final graph have at most one successor.
From the two previous remarks it follows that the final graph is made up from disjoint paths and disjoint circuits. Therefore the maximum number of arcs of the final graph is equal to its maximum number of vertices . So we can rewrite the graph property to and simplify to .
- Automaton
Figure 5.199.2 depicts the automaton associated with the constraint. To each item of the collection corresponds a signature variable that is equal to 1.
Figure 5.199.2. Automaton of the constraint