Global Constraint Catalog: Clength_last

5.216. length_last_sequence

DESCRIPTION

LINKS

AUTOMATON

Origin

Inspired by $𝚜𝚝𝚛𝚎𝚝𝚌𝚑_𝚙𝚊𝚝𝚑$

Constraint

$𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎 (𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙻𝙴𝙽$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙻𝙴𝙽 \geq 0

𝙻𝙴𝙽 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

$𝙻𝙴𝙽$ is the length of the maximum sequence of variables that take the same value that contains the last variable of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ (or 0 if the collection is empty).

Example

(1, 〈4, 4, 4, 5, 5, 4〉)

(6, 〈4, 4, 4, 4, 4, 4〉)

(5, 〈2, 4, 4, 4, 4, 4〉)

The first $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint holds since the sequence associated with the last value of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = 〈 4, 4, 4, 5, 5, 4 〉$ spans over a single variable.

Typical

𝙻𝙴𝙽 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

Symmetry

All occurrences of two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Functional dependency: $𝙻𝙴𝙽$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Reformulation

Without loss of generality let assume that the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = 〈 V_{1}, V_{2}, \dots, V_{n} 〉$ has more than one variable. By introducing $2 \cdot n - 1$ 0-1 variables, the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ constraint can be expressed in term of $2 \cdot n - 1$ reified constraints and one arithmetic constraint (i.e., a $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraint). We first introduce $n - 1$ variables that are respectively set to 1 if and only if two given consecutive variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are equal:

$B_{n - 1, n} \Leftrightarrow V_{n - 1} = V_{n}$ ,

$B_{n - 2, n - 1} \Leftrightarrow V_{n - 2} = V_{n - 1}$ ,

$\dots \dots \dots \dots \dots \dots \dots \dots \dots$

$B_{1, 2} \Leftrightarrow V_{1} = V_{2}$ .

We then introduce $n$ variables $A_{n}, A_{n - 1}, \dots, A_{1}$ that are respectively associated to the different sliding sequences ending on the last variable of the sequence $V_{1} V_{2} \dots V_{n}$ . Variable $A_{i}$ is set to 1 if and only if $V_{n} = V_{n - 1} = \dots = V_{i}$ :

$A_{n} = 1$ ,

$A_{n - 1} \Leftrightarrow B_{n - 1, n} \land A_{n},$

$A_{n - 2} \Leftrightarrow B_{n - 2, n - 1} \land A_{n - 1},$

$\dots \dots \dots \dots \dots \dots \dots \dots \dots$

$A_{1} \Leftrightarrow B_{1, 2} \land A_{2}$ .

Finally we state the following arithmetic constraint:

$𝙻𝙴𝙽 = A_{n} + A_{n - 1} + \dots + A_{1}$ .

Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7776	117649	2097152	43046721

Number of solutions for $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ : domains $0 . . n$

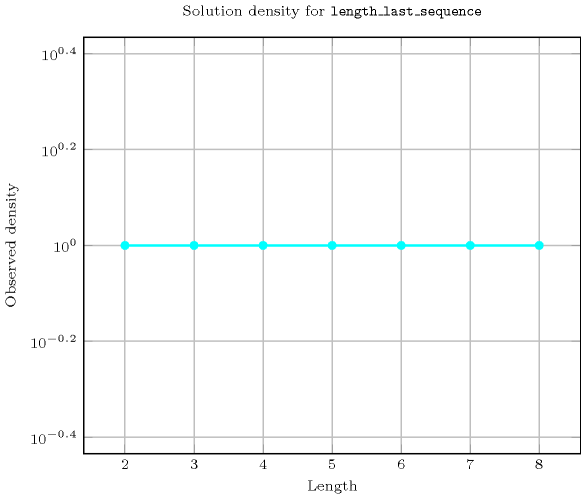
ctrs/length_last_sequence-1-tikz

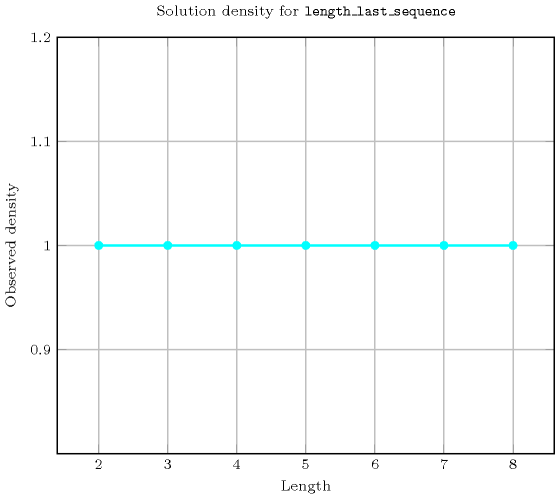
ctrs/length_last_sequence-2-tikz

Length (

n

)

Total

625

7776

117649

2097152

43046721

Parameter

value

500

6480

100842

1835008

38263752

100

1080

14406

229376

4251528

180

2058

28672

472392

294

3584

52488

448

5832

648

Solution count for $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ : domains $0 . . n$

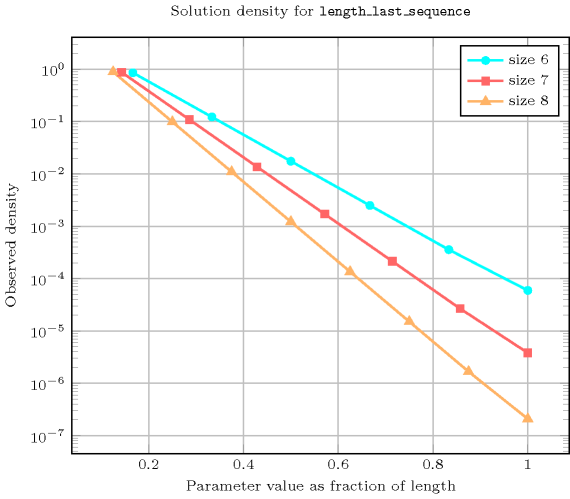
ctrs/length_last_sequence-3-tikz

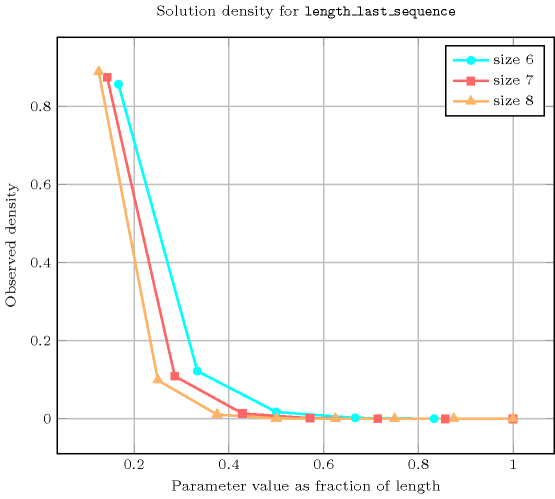
ctrs/length_last_sequence-4-tikz

Keywords

characteristic of a constraint: automaton, automaton with counters.

combinatorial object: sequence.

constraint arguments: reverse of a constraint, pure functional dependency.

constraint network structure: sliding cyclic(1) constraint network(2).

constraint type: value constraint, counting constraint.

filtering: glue matrix.

modelling: functional dependency.

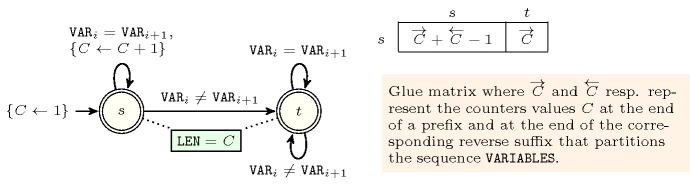
Automaton: Figure 5.216.1 depicts the automaton associated with the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint. To each pair of consecutive variables $({𝚅𝙰𝚁}_{i}, {𝚅𝙰𝚁}_{i + 1})$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ , ${𝚅𝙰𝚁}_{i + 1}$ and $S_{i}$ : ${𝚅𝙰𝚁}_{i} = {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i}$ .

Figure 5.216.1. Automaton of the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint when $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 2$

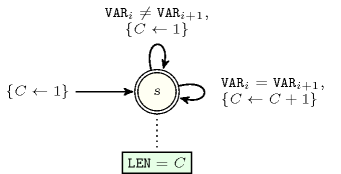
Figure 5.216.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint

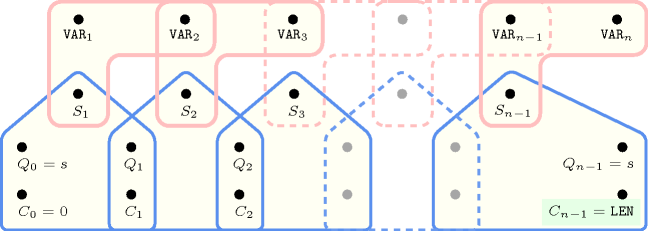
Figure 5.216.3. Automaton of the reverse of the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint (i.e., the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚏𝚒𝚛𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint) when $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 2$ and corresponding glue matrix between $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ and its reverse $𝚕𝚎𝚗𝚐𝚝𝚑_𝚏𝚒𝚛𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$

Global Constraint Catalog

5. Global Constraint Catalogue

5.216. length_last_sequence

Figure 5.216.1. Automaton of the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint when $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 2$

Figure 5.216.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.216. length_last_sequence

Figure 5.216.1. Automaton of the 𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎 constraint when |𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂|≥2

Figure 5.216.2. Hypergraph of the reformulation corresponding to the automaton of the 𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎 constraint

Figure 5.216.1. Automaton of the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint when $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 2$

Figure 5.216.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ constraint