Global Constraint Catalog: Cminimum

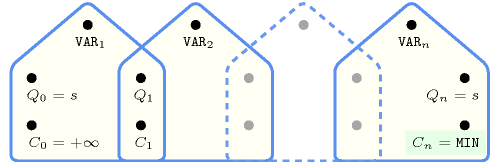
5.262. minimum

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

CHIP

Constraint

$𝚖𝚒𝚗𝚒𝚖𝚞𝚖 (𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonym

$𝚖𝚒𝚗$ .

Arguments

$𝙼𝙸𝙽$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

$𝙼𝙸𝙽$ is the minimum value of the collection of domain variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Example

(2, 〈3, 2, 7, 2, 6〉)

(7, 〈8, 8, 7, 8, 7〉)

The first $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint holds since its first argument $𝙼𝙸𝙽 = 2$ is set to the minimum value of the collection $〈 3, 2, 7, 2, 6 〉$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
All occurrences of two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped.
One and the same constant can be added to $𝙼𝙸𝙽$ as well as to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Functional dependency: $𝙼𝙸𝙽$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .
Aggregate: $𝙼𝙸𝙽 (𝚖𝚒𝚗)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ .

Usage

In some project scheduling problems one has to introduce dummy activities that correspond for instance to the starting time of a given set of activities. In this context one can use the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint to get the minimum starting time of a set of tasks.

Remark

Note that $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ is a constraint and not just a function that computes the minimum value of a collection of variables: potential values of $𝙼𝙸𝙽$ influence the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ , and reciprocally potential values that can be assigned to variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ influence $𝙼𝙸𝙽$ .

The $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint is called $𝚖𝚒𝚗$ in JaCoP (http://www.jacop.eu/).

Algorithm

A filtering algorithm for the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint is described in [Beldiceanu01].

The $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint is entailed if all the following conditions hold:

$𝙼𝙸𝙽$ is fixed.
At least one variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ is assigned value $𝙼𝙸𝙽$ .
All variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ have their minimum value greater than or equal to value $𝙼𝙸𝙽$ .

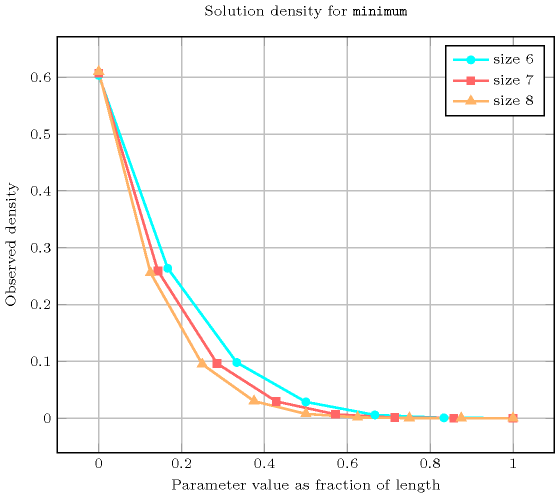
Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7776	117649	2097152	43046721

Number of solutions for $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ : domains $0 . . n$

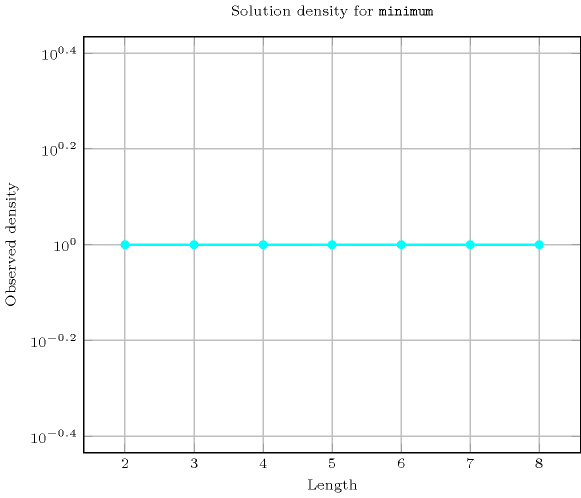
ctrs/minimum-1-tikz

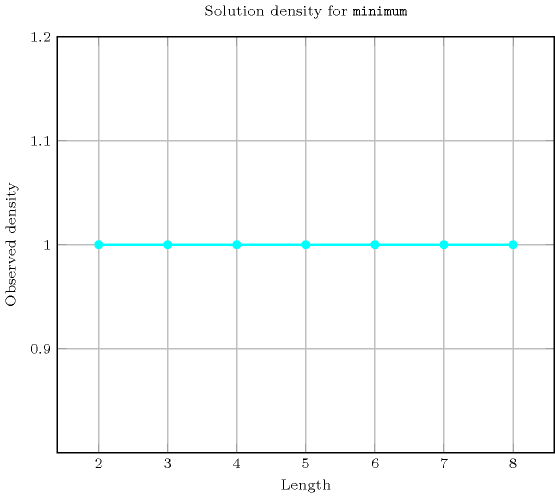
ctrs/minimum-2-tikz

Length (

n

)

Total

625

7776

117649

2097152

43046721

Parameter

value

369

4651

70993

1273609

26269505

175

2101

31031

543607

11012415

781

11529

201811

4085185

211

3367

61741

1288991

665

14197

325089

2059

58975

127

6305

255

Solution count for $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ : domains $0 . . n$

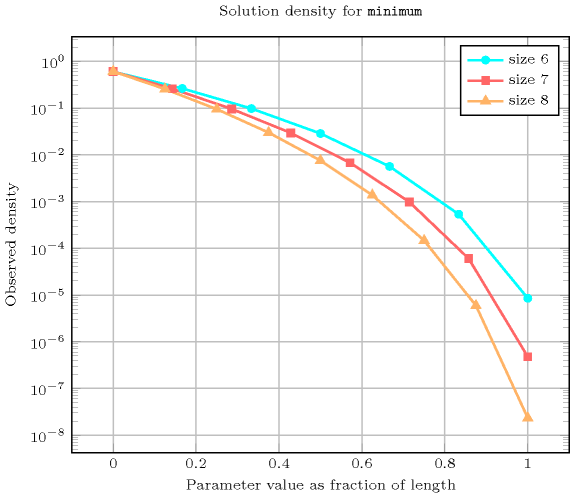
ctrs/minimum-3-tikz

ctrs/minimum-4-tikz

Systems

min in Choco, min in Gecode, min in JaCoP, minimum in MiniZinc, minimum in SICStus.

Used in

$𝚖𝚒𝚗𝚒𝚖𝚞𝚖_𝚐𝚛𝚎𝚊𝚝𝚎𝚛_𝚝𝚑𝚊𝚗$ , $𝚗𝚎𝚡𝚝_𝚎𝚕𝚎𝚖𝚎𝚗𝚝$ , $𝚗𝚎𝚡𝚝_𝚐𝚛𝚎𝚊𝚝𝚎𝚛_𝚎𝚕𝚎𝚖𝚎𝚗𝚝$ .

comparison swapped: $𝚖𝚊𝚡𝚒𝚖𝚞𝚖$ .

generalisation: $𝚖𝚒𝚗𝚒𝚖𝚞𝚖_𝚖𝚘𝚍𝚞𝚕𝚘$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \mod 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ ).

implied by: $𝚊𝚗𝚍$ .

implies: $𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚖𝚒𝚗_𝚖𝚊𝚡$ , $𝚒𝚗$ .

soft variant: $𝚖𝚒𝚗𝚒𝚖𝚞𝚖_𝚎𝚡𝚌𝚎𝚙𝚝_0$ (value 0 is ignored), $𝚘𝚙𝚎𝚗_𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ (open constraint).

specialisation: $𝚖𝚒𝚗_𝚗$ (minimum or order $𝚗$ replaced by absolute minimum).

uses in its reformulation: $𝚌𝚢𝚌𝚕𝚎$ .

Keywords

characteristic of a constraint: minimum, maxint, automaton, automaton without counters, reified automaton constraint.

constraint arguments: reverse of a constraint, pure functional dependency.

constraint network structure: centered cyclic(1) constraint network(1).

constraint type: order constraint.

filtering: glue matrix, arc-consistency, entailment.

modelling: functional dependency.

Cond. implications

$𝚖𝚒𝚗𝚒𝚖𝚞𝚖 (𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚏𝚒𝚛𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 𝙼𝙸𝙽$

and $𝚕𝚊𝚜𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 𝙼𝙸𝙽$

implies $𝚍𝚎𝚎𝚙𝚎𝚜𝚝_𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝙳𝙴𝙿𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

⋁ (\begin{matrix} 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚔𝚎𝚢 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚔𝚎𝚢, \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 < 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 \end{matrix})

Graph property(ies)

𝐎𝐑𝐃𝐄𝐑

(0, 𝙼𝙰𝚇𝙸𝙽𝚃, 𝚟𝚊𝚛) = 𝙼𝙸𝙽

Graph model

The condition $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚔𝚎𝚢 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚔𝚎𝚢$ holds if and only if $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1$ and $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2$ corresponds to the same vertex. It is used in order to enforce to keep all the vertices of the initial graph. $𝐎𝐑𝐃𝐄𝐑 (0, 𝙼𝙰𝚇𝙸𝙽𝚃, 𝚟𝚊𝚛)$ refers to the source vertices of the graph, i.e., those vertices that do not have any predecessor.

Parts (A) and (B) of Figure 5.262.1 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the $𝐎𝐑𝐃𝐄𝐑$ graph property, the vertices of rank 0 (without considering the loops) of the final graph are outlined with a thick circle.

Figure 5.262.1. Initial and final graph of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint


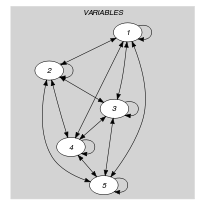
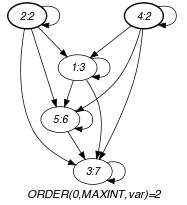
(a)	(b)

Automaton

Figure 5.262.2 depicts a first counter free deterministic automaton associated with the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint. Let ${𝚅𝙰𝚁}_{i}$ be the $i^{t h}$ variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. To each pair $(𝙼𝙸𝙽, {𝚅𝙰𝚁}_{i})$ corresponds a signature variable $S_{i}$ as well as the following signature constraint: $(𝙼𝙸𝙽 < {𝚅𝙰𝚁}_{i} \Leftrightarrow S_{i} = 0) \land (𝙼𝙸𝙽 = {𝚅𝙰𝚁}_{i} \Leftrightarrow S_{i} = 1) \land (𝙼𝙸𝙽 > {𝚅𝙰𝚁}_{i} \Leftrightarrow S_{i} = 2)$ .

Figure 5.262.2. Counter free automaton of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint

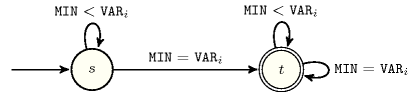
Figure 5.262.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint

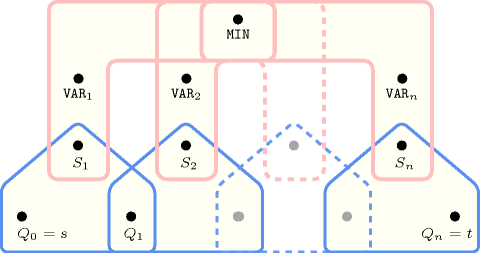
Figure 5.262.3 depicts a second counter free non deterministic automaton associated with the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint, where the argument $𝙼𝙸𝙽$ is also part of the sequence passed to the automaton.

Figure 5.262.4. Counter free non deterministic automaton of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ constraint assuming that the union of the domain of the variables is the set ${1, 2, 3, 4}$ and that the elements of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are first passed to the automaton followed by $𝙼𝙸𝙽$ (state $s_{i}$ means that no value strictly less than value $i$ was found and that value $i$ was already encountered at least once)

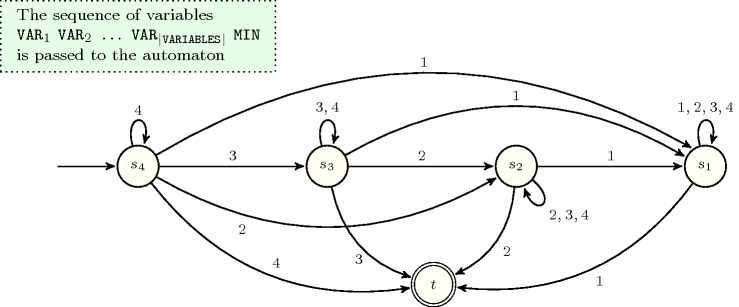
Figure 5.262.5. Hypergraph of the reformulation corresponding to the counter free non deterministic automaton of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint

Figure 5.262.6 depicts a third deterministic automaton with one counter associated with the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint, where the argument $𝙼𝙸𝙽$ is unified to the final value of the counter.

Figure 5.262.6. Automaton (with one counter) of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint and its glue matrix

Figure 5.262.7. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint: since all states variables $Q_{0}, Q_{1}, \dots, Q_{n}$ are fixed to the unique state $s$ of the automaton, the transitions constraints share only the counter variable $C$ and the constraint network is Berge-acyclic

Global Constraint Catalog

5. Global Constraint Catalogue

5.262. minimum

Figure 5.262.1. Initial and final graph of the 𝚖𝚒𝚗𝚒𝚖𝚞𝚖 constraint

Figure 5.262.2. Counter free automaton of the 𝚖𝚒𝚗𝚒𝚖𝚞𝚖 constraint

Figure 5.262.3. Hypergraph of the reformulation corresponding to the automaton of the 𝚖𝚒𝚗𝚒𝚖𝚞𝚖 constraint

Figure 5.262.5. Hypergraph of the reformulation corresponding to the counter free non deterministic automaton of the 𝚖𝚒𝚗𝚒𝚖𝚞𝚖 constraint

Figure 5.262.6. Automaton (with one counter) of the 𝚖𝚒𝚗𝚒𝚖𝚞𝚖 constraint and its glue matrix

Figure 5.262.1. Initial and final graph of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint

Figure 5.262.2. Counter free automaton of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint

Figure 5.262.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint

Figure 5.262.5. Hypergraph of the reformulation corresponding to the counter free non deterministic automaton of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint

Figure 5.262.6. Automaton (with one counter) of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint and its glue matrix