5.275. next_element
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
N. Beldiceanu
- Constraint
- Arguments
- Restrictions
- Purpose
is the smallest entry of strictly greater than containing value .
- Example
-
The constraint holds since 3 is the smallest entry located after entry 2 that contains value 9.
- Typical
- Usage
Originally introduced for modelling the fact that a nucleotide has to be consumed as soon as possible at cycle after a given cycle represented by variable .
- See also
related: (identify an element in a table), (allow to iterate over the values of a table).
- Keywords
characteristic of a constraint: minimum, automaton, automaton without counters, reified automaton constraint, derived collection.
constraint network structure: centered cyclic(3) constraint network(1).
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Sets
-
- Constraint(s) on sets
- Graph model
Parts (A) and (B) of Figure 5.275.1 respectively show the initial and final graph associated with the second graph constraint of the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold.
Figure 5.275.1. Initial and final graph of the constraint
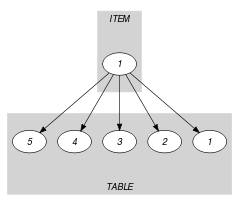
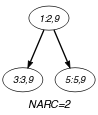
(a) (b)
- Automaton
Figure 5.275.2 depicts the automaton associated with the constraint. Let and respectively be the and the attributes of the item of the collections. To each quintuple corresponds a signature variable as well as the following signature constraint:
.
The automaton is constructed in order to fulfil the following conditions:
We look for an item of the collection such that and and ,
There should not exist any item of the collection such that and and .
Figure 5.275.2. Automaton of the constraint
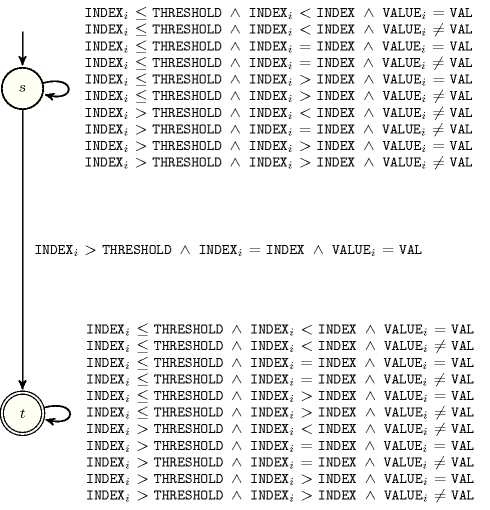
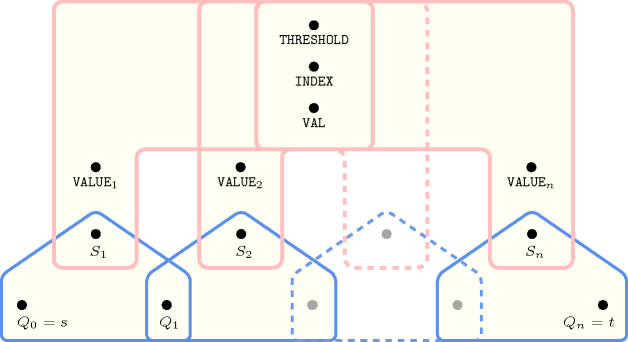
Figure 5.275.3. Hypergraph of the reformulation corresponding to the automaton of the constraint