Global Constraint Catalog: Cnot

5.283. not_in

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚒𝚗$ .

Constraint

$𝚗𝚘𝚝_𝚒𝚗 (𝚅𝙰𝚁, 𝚅𝙰𝙻𝚄𝙴𝚂)$

Arguments

$𝚅𝙰𝚁$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝙻𝚄𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

Purpose

Enforce $𝚅𝙰𝚁$ to be assigned a value different from the values of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection.

Example

(2, 〈1, 3〉)

The constraint $𝚗𝚘𝚝_𝚒𝚗$ holds since the value of its first argument $𝚅𝙰𝚁 = 2$ does not occur within the collection $〈 1, 3 〉$ .

Typical

| 𝚅𝙰𝙻𝚄𝙴𝚂 | > 1

Symmetries

Items of $𝚅𝙰𝙻𝚄𝙴𝚂$ are permutable.
One and the same constant can be added to $𝚅𝙰𝚁$ as well as to the $𝚟𝚊𝚕$ attribute of all items of $𝚅𝙰𝙻𝚄𝙴𝚂$ .

Arg. properties

Contractible wrt. $𝚅𝙰𝙻𝚄𝙴𝚂$ .

Remark

Entailment occurs immediately after posting this constraint and removing all values in $𝚅𝙰𝙻𝚄𝙴𝚂$ from $𝚅𝙰𝚁$ .

Systems

notMember in Choco, rel in Gecode.

Used in

$𝚐𝚛𝚘𝚞𝚙$ .

See also

negation: $𝚒𝚗$ .

Keywords

characteristic of a constraint: disequality, automaton, automaton without counters, reified automaton constraint, derived collection.

constraint arguments: unary constraint.

constraint network structure: centered cyclic(1) constraint network(1).

constraint type: value constraint.

filtering: arc-consistency, entailment.

modelling: excluded, domain definition.

Derived Collection

𝚌𝚘𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛), [𝚒𝚝𝚎𝚖 (𝚟𝚊𝚛 - 𝚅𝙰𝚁)])

Arc input(s): $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ $𝚅𝙰𝙻𝚄𝙴𝚂$
Arc generator: $𝑃𝑅𝑂𝐷𝑈𝐶𝑇$ $\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, 𝚟𝚊𝚕𝚞𝚎𝚜)$
Arc arity
Arc constraint(s): $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚟𝚊𝚛 = 𝚟𝚊𝚕𝚞𝚎𝚜 . 𝚟𝚊𝚕$
Graph property(ies): $𝐍𝐀𝐑𝐂$ $= 0$
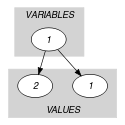
Graph model: Figure 5.283.1 shows the initial graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂 = 0$ graph property the corresponding final graph is empty.

Figure 5.283.1. Initial graph of the $𝚗𝚘𝚝_𝚒𝚗$ constraint (the final graph is empty)
Signature: Since 0 is the smallest number of arcs of the final graph we can rewrite $𝐍𝐀𝐑𝐂 = 0$ to $𝐍𝐀𝐑𝐂 \leq 0$ . This leads to simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\underset{̲}{𝐍𝐀𝐑𝐂}$ .

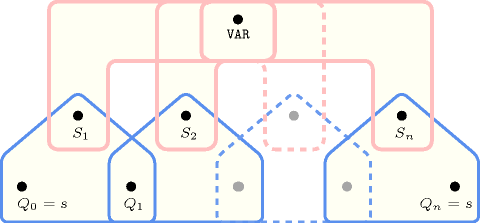
Automaton: Figure 5.283.2 depicts the automaton associated with the $𝚗𝚘𝚝_𝚒𝚗$ constraint. Let ${𝚅𝙰𝙻}_{i}$ be the $𝚟𝚊𝚕$ attribute of the $i^{t h}$ item of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection. To each pair $(𝚅𝙰𝚁, {𝚅𝙰𝙻}_{i})$ corresponds a 0-1 signature variable $S_{i}$ as well as the following signature constraint: $𝚅𝙰𝚁 = {𝚅𝙰𝙻}_{i} \Leftrightarrow S_{i}$ .

Figure 5.283.2. Automaton of the $𝚗𝚘𝚝_𝚒𝚗$ constraint

Figure 5.283.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚗𝚘𝚝_𝚒𝚗$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.283. not_in

Figure 5.283.1. Initial graph of the $𝚗𝚘𝚝_𝚒𝚗$ constraint (the final graph is empty)

Figure 5.283.2. Automaton of the $𝚗𝚘𝚝_𝚒𝚗$ constraint

Figure 5.283.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚗𝚘𝚝_𝚒𝚗$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.283. not_in

Figure 5.283.1. Initial graph of the 𝚗𝚘𝚝_𝚒𝚗 constraint (the final graph is empty)

Figure 5.283.2. Automaton of the 𝚗𝚘𝚝_𝚒𝚗 constraint

Figure 5.283.3. Hypergraph of the reformulation corresponding to the automaton of the 𝚗𝚘𝚝_𝚒𝚗 constraint

Figure 5.283.1. Initial graph of the $𝚗𝚘𝚝_𝚒𝚗$ constraint (the final graph is empty)

Figure 5.283.2. Automaton of the $𝚗𝚘𝚝_𝚒𝚗$ constraint

Figure 5.283.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚗𝚘𝚝_𝚒𝚗$ constraint