5.313. orths_are_connected
| DESCRIPTION | LINKS | GRAPH |
- Origin
N. Beldiceanu
- Constraint
- Type
- Argument
- Restrictions
- Purpose
There should be a single group of connected orthotopes. Two orthotopes touch each other (i.e., are connected) if they overlap in all dimensions except one, and if, for the dimension where they do not overlap, the distance between the two orthotopes is equal to 0.
- Example
-
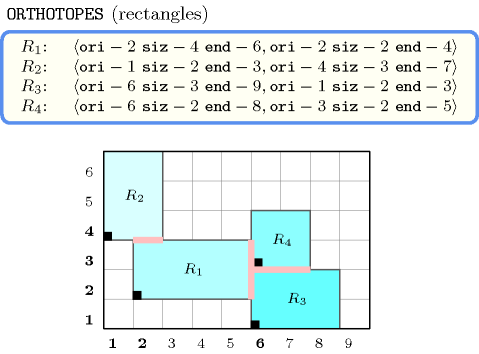
Figure 5.313.1 shows the rectangles associated with the example. One can note that:
Rectangle 2 touch rectangle 1,
Rectangle 1 touch rectangle 2, rectangle 3 and rectangle 4,
Rectangle 4 touch rectangle 1 and rectangle 3,
Rectangle 3 touch rectangle 1 and rectangle 4.
Consequently, since we have a single group of connected rectangles, the constraint holds.
Figure 5.313.1. The four connected rectangles of the Example slot: contacts between rectangles are shown in pink
- Typical
- Symmetries
Items of are permutable.
Items of are permutable (same permutation used).
One and the same constant can be added to the and attributes of all items of .
- Usage
In floor planning problem there is a typical constraint, that states that one should be able to access every room from any room.
- See also
implies: .
- Keywords
geometry: geometrical constraint, touch, contact, non-overlapping, orthotope.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
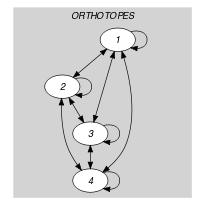
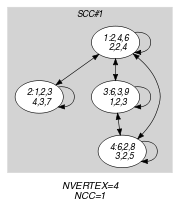
Parts (A) and (B) of Figure 5.313.2 respectively show the initial and final graph associated with the Example slot.Since we use the graph property the vertices of the final graph are stressed in bold. Since we also use the graph property we show the unique connected component of the final graph. An arc between two vertices indicates that two rectangles are in contact.
Figure 5.313.2. Initial and final graph of the constraint
(a) (b) - Signature
Since the first graph constraint uses the arc generator on the collection the corresponding initial graph contains arcs. Therefore the final graph of the first graph constraint contains at most arcs and we can rewrite to . So we can simplify to .
Consider now the second graph constraint. Since its corresponding initial graph contains vertices, its final graph has a maximum number of vertices also equal to . Therefore we can rewrite to and simplify to . From the graph property and from the restriction the final graph is not empty. Therefore it contains at least one connected component. So we can rewrite to and simplify to .