Global Constraint Catalog: Csliding

5.351. sliding_sum

DESCRIPTION

LINKS

GRAPH

Origin

CHIP

Constraint

$𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖 (𝙻𝙾𝚆, 𝚄𝙿, 𝚂𝙴𝚀, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonym

$𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ .

Arguments

$𝙻𝙾𝚆$	$𝚒𝚗𝚝$
$𝚄𝙿$	$𝚒𝚗𝚝$
$𝚂𝙴𝚀$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚄𝙿 \geq 𝙻𝙾𝚆

𝚂𝙴𝚀 > 0

𝚂𝙴𝚀 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Constrains all sequences of $𝚂𝙴𝚀$ consecutive variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ so that the sum of the variables belongs to interval $[𝙻𝙾𝚆, 𝚄𝙿]$ .

Example

(3, 7, 4, 〈1, 4, 2, 0, 0, 3, 4〉)

The example considers all sliding sequences of $𝚂𝙴𝚀 = 4$ consecutive values of $〈 1, 4, 2, 0, 0, 3, 4 〉$ collection and constraints the sum to be in $[𝙻𝙾𝚆, 𝚄𝙿] = [3, 7]$ . The $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ constraint holds since the sum associated with the corresponding subsequences $1420$ , $4200$ , $2003$ , and $0034$ are respectively 7, 6, 5 and 7.

Typical

𝙻𝙾𝚆 \geq 0

𝚄𝙿 > 0

𝚂𝙴𝚀 > 1

𝚂𝙴𝚀 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq 0

𝚄𝙿 <

𝚜𝚞𝚖

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)

Symmetry

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝚂𝙴𝚀 = 1$ .
Prefix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .
Suffix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Algorithm

Beldiceanu and Carlsson [BeldiceanuCarlsson01] have proposed a first incomplete filtering algorithm for the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ constraint. In 2008, Maher et al. showed in [MaherNarodytskaQuimperWalsh08] that the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ constraint has a solution “if and only there are no negative cycles in the flow graph associated with the dual linear program” that encodes the conjunction of inequalities. They derive a bound-consistency filtering algorithm from this fact.

Systems

sliding_sum in MiniZinc.

part of system of constraints: $𝚜𝚞𝚖_𝚌𝚝𝚛$ .

soft variant: $𝚛𝚎𝚕𝚊𝚡𝚎𝚍_𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ .

used in graph description: $𝚜𝚞𝚖_𝚌𝚝𝚛$ .

Keywords

characteristic of a constraint: hypergraph, sum.

combinatorial object: sequence.

constraint type: decomposition, sliding sequence constraint, system of constraints.

filtering: linear programming, flow, bound-consistency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗

Arc arity

𝚂𝙴𝚀

Arc constraint(s)

•

𝚜𝚞𝚖_𝚌𝚝𝚛

(𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗, \geq, 𝙻𝙾𝚆)

•

𝚜𝚞𝚖_𝚌𝚝𝚛

(𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗, \leq, 𝚄𝙿)

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1

Graph model

We use $𝚜𝚞𝚖_𝚌𝚝𝚛$ as an arc constraint. $𝚜𝚞𝚖_𝚌𝚝𝚛$ takes a collection of domain variables as its first argument.

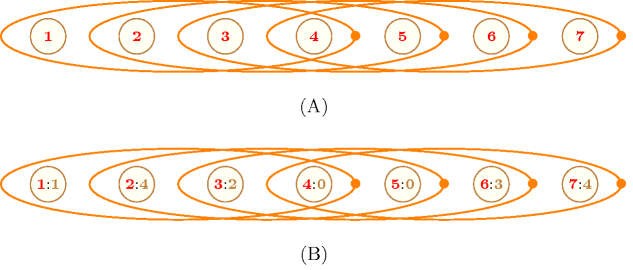
Parts (A) and (B) of Figure 5.351.1 respectively show the initial and final graph associated with the Example slot. Since all arc constraints hold (i.e., because of the graph property $𝐍𝐀𝐑𝐂 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1$ ) the final graph corresponds to the initial graph.

Figure 5.351.1. (A) Initial and (B) final graph of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ $(3, 7, 4, 〈 1, 4, 2, 0, 0, 3, 4 〉)$ constraint of the Example slot where each ellipse represents an hyperedge involving $𝚂𝙴𝚀 = 4$ vertices (e.g., the first ellipse represents the constraint $1 + 4 + 2 + 0 \in [3, 7]$ )

Signature

Since we use the $𝑃𝐴𝑇𝐻$ arc generator with an arity of $𝚂𝙴𝚀$ on the items of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection, the expression $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1$ corresponds to the maximum number of arcs of the final graph. Therefore we can rewrite the graph property $𝐍𝐀𝐑𝐂 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1$ to $𝐍𝐀𝐑𝐂 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝚂𝙴𝚀 + 1$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.351. sliding_sum

Figure 5.351.1. (A) Initial and (B) final graph of the 𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖(3,7,4,〈1,4,2,0,0,3,4〉) constraint of the Example slot where each ellipse represents an hyperedge involving 𝚂𝙴𝚀=4 vertices (e.g., the first ellipse represents the constraint 1+4+2+0∈[3,7])