5.353. sliding_time_window_from_start
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
The sum of the intersections of all the tasks of the collection with interval is less than or equal to .
- Example
-
The intersections of tasks , , and with interval are respectively equal to 3, 1, and 2 (i.e., the three tasks of the collection are in fact included within interval ). Consequently, the constraint holds since the sum of these intersections does not exceed the value of its second argument .
- Typical
- Symmetries
can be decreased.
can be increased.
Items of are permutable.
can be decreased to any value .
One and the same constant can be added to as well as to the attribute of all items of .
- Arg. properties
Contractible wrt. .
- Reformulation
- Used in
- Keywords
characteristic of a constraint: derived collection.
constraint type: sliding sequence constraint, temporal constraint.
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Since we use the arc constraint the final and the initial graph are identical. The unique source of the final graph corresponds to the interval . Each sink of the final graph represents a given task of the collection. We associate to each arc the value given by the intersection of the task associated with one of the extremities of the arc with the time window . Finally, the graph property sums up all the valuations of the arcs and check that it does not exceed a given limit.
Parts (A) and (B) of Figure 5.353.1 respectively show the initial and final graph associated with the Example slot. To each arc of the final graph we associate the intersection of the corresponding sink task with interval . The constraint holds since the sum of the previous intersections does not exceed .
Figure 5.353.1. Initial and final graph of the constraint
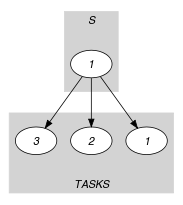
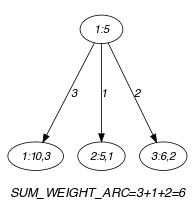
(a) (b)