Global Constraint Catalog: Csoft_alldifferent

5.360. soft_alldifferent_var

DESCRIPTION

LINKS

GRAPH

Origin

[PetitReginBessiere01]

Constraint

$𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛 (𝙲, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonyms

$𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏_𝚟𝚊𝚛$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝_𝚟𝚊𝚛$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏_𝚖𝚒𝚗_𝚟𝚊𝚛$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚖𝚒𝚗_𝚟𝚊𝚛$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝_𝚖𝚒𝚗_𝚟𝚊𝚛$ .

Arguments

$𝙲$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙲 \geq 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

$𝙲$ is greater than or equal to the minimum number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ for which the value needs to be changed in order that all variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ take a distinct value.

Example

(3, 〈5, 1, 9, 1, 5, 5〉)

(1, 〈5, 1, 9, 6, 5, 3〉)

(0, 〈8, 1, 9, 6, 5, 3〉)

Within the collection $〈 5, 1, 9, 1, 5, 5 〉$ of the first example, 3 and 2 items are respectively fixed to values 5 and 1. Therefore one must change the values of at least $(3 - 1) + (2 - 1) = 3$ items to get back to 6 distinct values. Consequently, the corresponding $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ constraint holds since its first argument $𝙲$ is greater than or equal to 3.

Typical

𝙲 > 0

2 * 𝙲 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚜𝚘𝚖𝚎_𝚎𝚚𝚞𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)

Symmetries

$𝙲$ can be increased.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
All occurrences of two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Usage

A soft $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint.

Remark

Since it focus on the soft aspect of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint, the original article [PetitReginBessiere01], which introduce this constraint, describes how to evaluate the minimum value of $𝙲$ and how to prune according to the maximum value of $𝙲$ .

The $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ constraint is called $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏_𝚖𝚒𝚗_𝚟𝚊𝚛$ in [HebrardMarxSullivanRazgon09].

Algorithm

A first filtering algorithm presented in [PetitReginBessiere01] achieves arc-consistency. A second filtering algorithm also achieving arc-consistency is described in [Cymer12], [CymerPhD13].

Reformulation

By introducing a variable $M$ that gives the number of distinct values used by variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ , the $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ $(𝙲, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ constraint can be expressed as a conjunction of the $𝚗𝚟𝚊𝚕𝚞𝚎$ $(M, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ constraint and of the linear constraint $𝙲 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - M$ .

Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	24	212	2470	35682	614600	12286024	279472266

Number of solutions for $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ : domains $0 . . n$

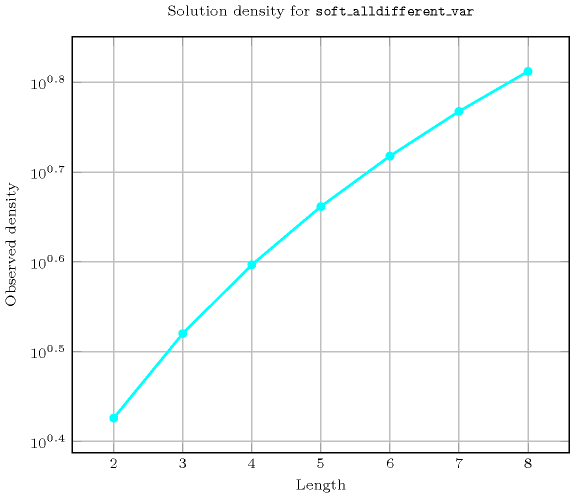
ctrs/soft_alldifferent_var-1-tikz

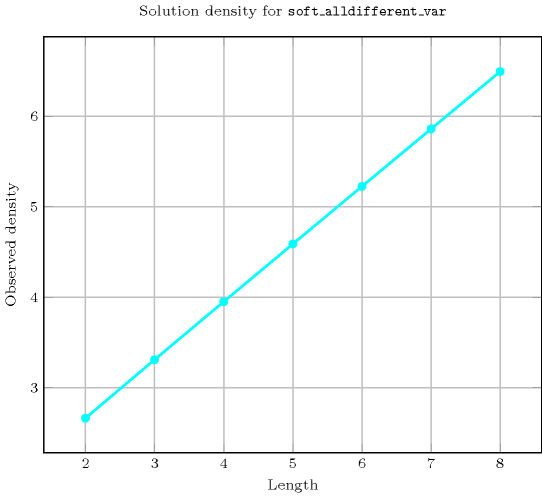
ctrs/soft_alldifferent_var-2-tikz

Length (

n

)

Total

212

2470

35682

614600

12286024

279472266

Parameter

value

120

720

5040

40320

362880

480

4320

42840

463680

5443200

620

7320

97440

1404480

21530880

625

7770

116340

1992480

37406880

625

7776

117642

2093616

42550704

7776

117649

2097144

43037568

117649

2097152

43046712

2097152

43046721

Solution count for $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ : domains $0 . . n$

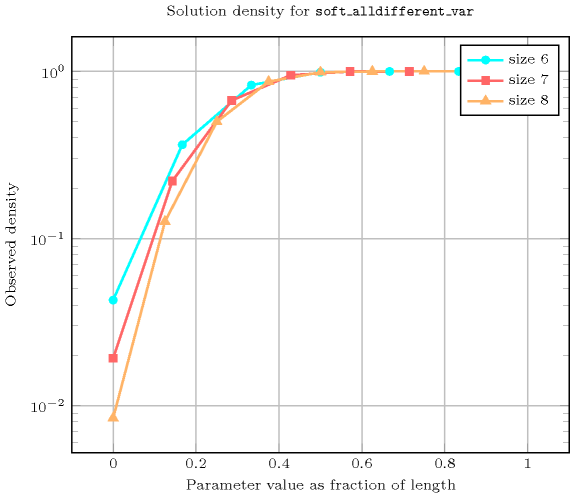
ctrs/soft_alldifferent_var-3-tikz

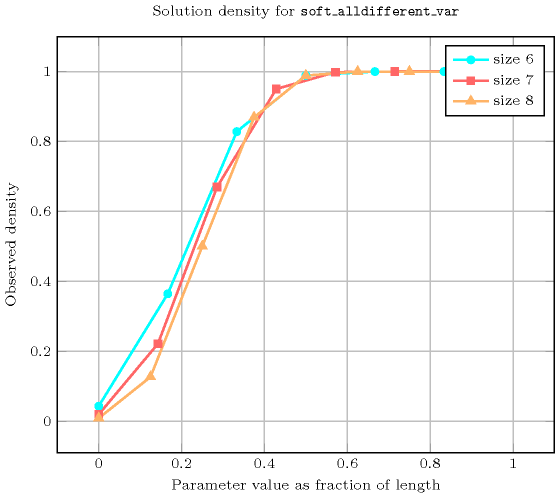
ctrs/soft_alldifferent_var-4-tikz

hard version: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

implied by: $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ , $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚖𝚘𝚍𝚞𝚕𝚘$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚝𝚛$ .

Keywords

characteristic of a constraint: all different, disequality.

constraint type: soft constraint, value constraint, relaxation, variable-based violation measure.

filtering: bipartite matching.

final graph structure: strongly connected component, equivalence.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐒𝐂𝐂

\geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝙲

Graph model

We generate a clique with binary equalities constraints between each pairs of vertices (this include an arc between a vertex and itself) and we state that $𝙲$ is equal to the difference between the total number of variables and the number of strongly connected components.

Parts (A) and (B) of Figure 5.360.1 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the $𝐍𝐒𝐂𝐂$ graph property we show the different strongly connected components of the final graph. Each strongly connected component of the final graph includes all variables that take the same value. Since we have 6 variables and 3 strongly connected components the cost variable $𝙲$ is greater than or equal to $6 - 3$ .

Figure 5.360.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ constraint


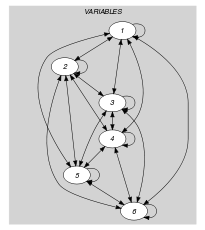
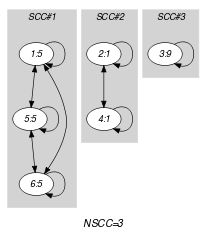
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.360. soft_alldifferent_var

Figure 5.360.1. Initial and final graph of the 𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛 constraint

Figure 5.360.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ constraint