5.370. some_equal
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, , , , .
- Argument
- Restrictions
- Purpose
Enforce at least two variables of the collection to be assigned the same value.
- Example
-
The constraint holds since the first and the third variables are both assigned the same value 1.
- Typical
- Symmetries
Items of are permutable.
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
- Arg. properties
Extensible wrt. .
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 3 40 505 7056 112609 2056832 42683841 Number of solutions for : domains
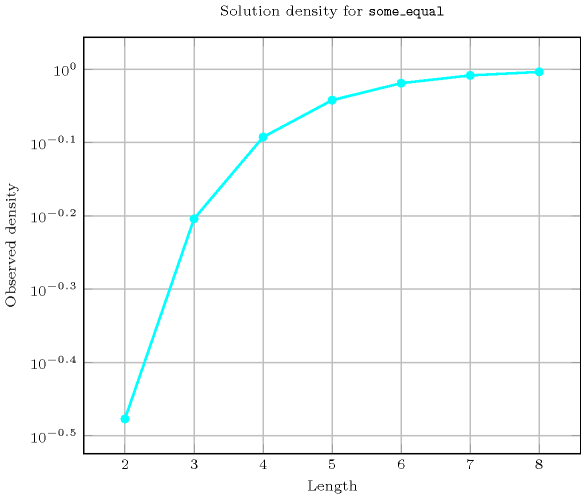
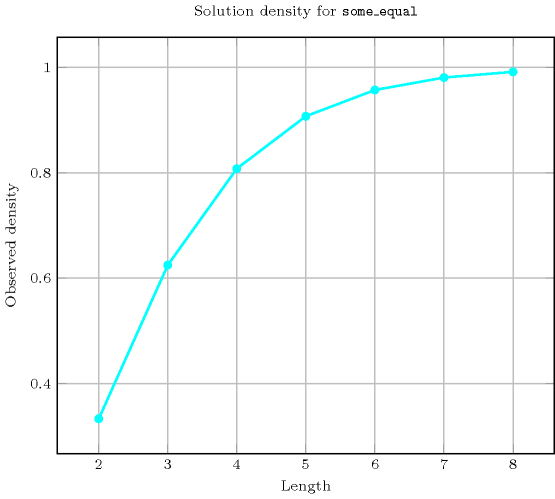
- Used in
- See also
- Keywords
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
We generate a clique with an equality constraint between each pair of distinct vertices and state that the number of arcs of the final graph should be strictly greater than 0.
Parts (A) and (B) of Figure 5.370.1 respectively show the initial and final graph associated with the Example slot. The constraint holds since the final graph has at one arc, i.e. two variables are assigned the same value.
Figure 5.370.1. Initial and final graph of the constraint
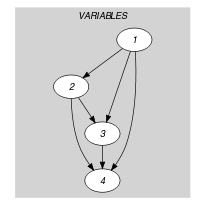
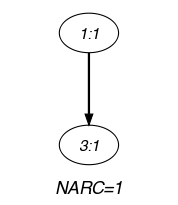
(a) (b)