Global Constraint Catalog: Csort

5.371. sort

DESCRIPTION

LINKS

GRAPH

Origin

[OlderSwinkelsEmden95]

Constraint

$𝚜𝚘𝚛𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$

Synonyms

$𝚜𝚘𝚛𝚝𝚎𝚍𝚗𝚎𝚜𝚜$ , $𝚜𝚘𝚛𝚝𝚎𝚍$ , $𝚜𝚘𝚛𝚝𝚒𝚗𝚐$ .

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

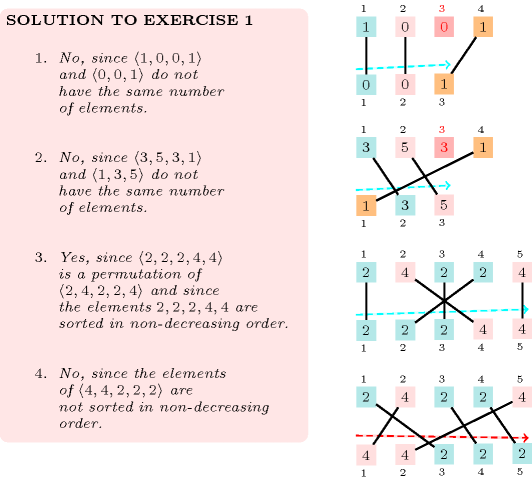
Purpose

First, the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ correspond to a permutation of the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ . Second, the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are sorted in increasing order.

Example

(〈1, 9, 1, 5, 2, 1〉, 〈1, 1, 1, 2, 5, 9〉)

The $𝚜𝚘𝚛𝚝$ constraint holds since:

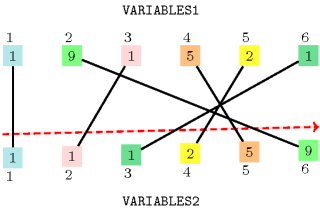
Values 1, 2, 5 and 9 have the same number of occurrences within both collections $〈 1, 9, 1, 5, 2, 1 〉$ and $〈 1, 1, 1, 2, 5, 9 〉$ . Figure 5.371.1 illustrates this correspondence.
The items of collection $〈 1, 1, 1, 2, 5, 9 〉$ are sorted in increasing order.

Figure 5.371.1. Illustration of the correspondence between the items of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections of the Example slot (note that the items of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are sorted in increasing order)

All solutions

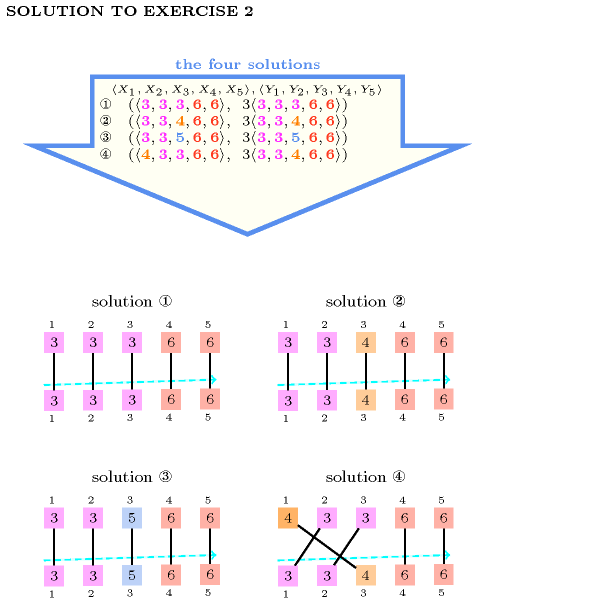
Figure 5.371.2 gives all solutions to the following non ground instance of the $𝚜𝚘𝚛𝚝$ constraint: $V_{1} \in [2, 3]$ , $V_{2} \in [2, 3]$ , $V_{3} \in [1, 2]$ , $V_{4} \in [4, 5]$ , $V_{5} \in [2, 4]$ , $S_{1} \in [2, 3]$ , $S_{2} \in [2, 3]$ , $S_{3} \in [1, 3]$ , $S_{4} \in [4, 5]$ , $S_{5} \in [2, 5]$ , $𝚜𝚘𝚛𝚝$ $(〈 V_{1}, V_{2}, V_{3}, V_{4}, V_{5} 〉, 〈 S_{1}, S_{2}, S_{3}, S_{4}, S_{5} 〉)$ .

Figure 5.371.2. All solutions corresponding to the non ground example of the $𝚜𝚘𝚛𝚝$ constraint of the All solutions slot

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
One and the same constant can be added to the $𝚟𝚊𝚛$ attributes of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .

Arg. properties

Functional dependency: $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .

Usage

The main usage of the $𝚜𝚘𝚛𝚝$ constraint, that was not foreseen when the $𝚜𝚘𝚛𝚝$ constraint was invented, is its use in many reformulations. Many constraints involving one or several collections of variables become much simpler to express when the variables of these collections are sorted. In addition these reformulations typically have a size that is linear in the number of variables of the original constraint. This justifies why the $𝚜𝚘𝚛𝚝$ constraint is considered to be a core constraint. As illustrative examples of these types of reformulations we successively consider the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ and the $𝚜𝚊𝚖𝚎$ constraints:

The $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ $(〈 v_{1}, v_{2}, \dots, v_{n} 〉)$ constraint can be reformulated as the conjunction $𝚜𝚘𝚛𝚝$ $(〈 v_{1}, v_{2}, \dots, v_{n} 〉, 〈 w_{1}, w_{2}, \dots, w_{n} 〉) \land$ $𝚜𝚝𝚛𝚒𝚌𝚝𝚕𝚢_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐$ $(〈 w_{1}, w_{2}, \dots, w_{n} 〉)$ .
The $𝚜𝚊𝚖𝚎$ $(〈 u_{1}, u_{2}, \dots, u_{n} 〉, 〈 v_{1}, v_{2}, \dots, v_{n} 〉)$ constraint can be reformulated as the conjunction $𝚜𝚘𝚛𝚝$ $(〈 u_{1}, u_{2}, \dots, u_{n} 〉, 〈 w_{1}, w_{2}, \dots, w_{n} 〉) \land$ $𝚜𝚘𝚛𝚝$ $(〈 v_{1}, v_{2}, \dots, v_{n} 〉, 〈 w_{1}, w_{2}, \dots, w_{n} 〉)$ .

Remark

A variant of this constraint called $𝚜𝚘𝚛𝚝_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ was introduced in [Zhou97]. In this variant an additional list of domain variables represents the permutation that allows to go from $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ to $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .

Algorithm

[GuernalecColmerauer97], [MehlhornThiel00].

Systems

sorting in Choco, sorted in Gecode, sort in MiniZinc, sorting in SICStus.

See also

generalisation: $𝚜𝚘𝚛𝚝_𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ ( $𝙿𝙴𝚁𝙼𝚄𝚃𝙰𝚃𝙸𝙾𝙽$ parameter added).

implies: $𝚕𝚎𝚡_𝚐𝚛𝚎𝚊𝚝𝚎𝚛𝚎𝚚$ , $𝚜𝚊𝚖𝚎$ .

uses in its reformulation: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ , $𝚜𝚊𝚖𝚎$ .

Keywords

characteristic of a constraint: core, sort.

combinatorial object: permutation.

constraint arguments: constraint between two collections of variables, pure functional dependency.

filtering: bound-consistency.

modelling: functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

• for all connected components:

𝐍𝐒𝐎𝐔𝐑𝐂𝐄

=

𝐍𝐒𝐈𝐍𝐊

•

𝐍𝐒𝐎𝐔𝐑𝐂𝐄

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |

•

𝐍𝐒𝐈𝐍𝐊

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 \leq 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | - 1

Graph model

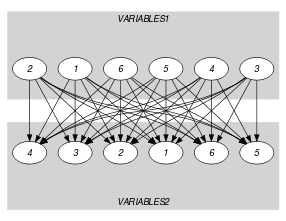
Parts (A) and (B) of Figure 5.371.3 respectively show the initial and final graph associated with the first graph constraint of the Example slot. Since it uses the $𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ and $𝐍𝐒𝐈𝐍𝐊$ graph properties, the source and sink vertices of this final graph are stressed with a double circle. Since there is a constraint on each connected component of the final graph we also show the different connected components. The $𝚜𝚘𝚛𝚝$ constraint holds since:

Each connected component of the final graph of the first graph constraint has the same number of sources and of sinks.
The number of sources of the final graph of the first graph constraint is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |$ .
The number of sinks of the final graph of the first graph constraint is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ .
Finally the second graph constraint holds also since its corresponding final graph contains exactly $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 - 1 |$ arcs: all the inequalities constraints between consecutive variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ holds.

Figure 5.371.3. Initial and final graph of the $𝚜𝚘𝚛𝚝$ constraint

(a)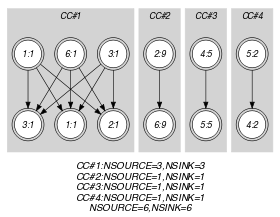

(b)

Signature

Consider the first graph constraint. Since the initial graph contains only sources and sinks, and since isolated vertices are eliminated from the final graph, we make the following observations:

Sources of the initial graph cannot become sinks of the final graph,
Sinks of the initial graph cannot become sources of the final graph.

From the previous observations and since we use the $𝑃𝑅𝑂𝐷𝑈𝐶𝑇$ arc generator on the collections $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ , we have that the maximum number of sources and sinks of the final graph is respectively equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |$ and $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ . Therefore we can rewrite $𝐍𝐒𝐎𝐔𝐑𝐂𝐄 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |$ to $𝐍𝐒𝐎𝐔𝐑𝐂𝐄 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |$ and simplify $\underset{̲}{\bar{𝐍𝐒𝐎𝐔𝐑𝐂𝐄}}$ to $\bar{𝐍𝐒𝐎𝐔𝐑𝐂𝐄}$ . In a similar way, we can rewrite $𝐍𝐒𝐈𝐍𝐊 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ to $𝐍𝐒𝐈𝐍𝐊 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ and simplify $\underset{̲}{\bar{𝐍𝐒𝐈𝐍𝐊}}$ to $\bar{𝐍𝐒𝐈𝐍𝐊}$ .

Consider now the second graph constraint. Since we use the $𝑃𝐴𝑇𝐻$ arc generator with an arity of 2 on the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collection, the maximum number of arcs of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | - 1$ . Therefore we can rewrite the graph property $𝐍𝐀𝐑𝐂 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | - 1$ to $𝐍𝐀𝐑𝐂 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | - 1$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Quiz

$𝚜𝚘𝚛𝚝$ : checking whether a ground instance holds or not ctrs/sort-3-tikz

$𝚜𝚘𝚛𝚝$ : finding all solutions ctrs/sort-4-tikz

ctrs/sort-5-tikz

ctrs/sort-6-tikz

Global Constraint Catalog

5. Global Constraint Catalogue

5.371. sort

Figure 5.371.1. Illustration of the correspondence between the items of the 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂1 and of the 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂2 collections of the Example slot (note that the items of the 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂2 are sorted in increasing order)

Figure 5.371.2. All solutions corresponding to the non ground example of the 𝚜𝚘𝚛𝚝 constraint of the All solutions slot

Figure 5.371.3. Initial and final graph of the 𝚜𝚘𝚛𝚝 constraint

Figure 5.371.2. All solutions corresponding to the non ground example of the $𝚜𝚘𝚛𝚝$ constraint of the All solutions slot

Figure 5.371.3. Initial and final graph of the $𝚜𝚘𝚛𝚝$ constraint