5.403. tree
| DESCRIPTION | LINKS | GRAPH |
- Origin
N. Beldiceanu
- Constraint
- Arguments
- Restrictions
- Purpose
Given a digraph described by the collection, cover by a set of trees in such a way that each vertex of belongs to one distinct tree. The edges of the trees are directed from their leaves to their respective roots.
- Example
-
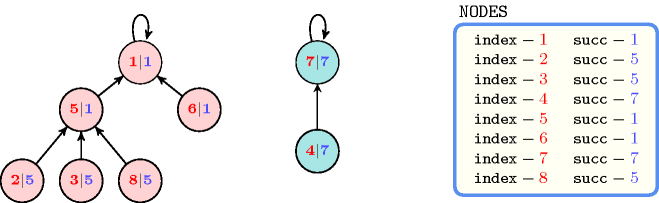
The first constraint holds since the graph associated with the items of the collection corresponds to two trees (i.e., ): each tree respectively involves the vertices and . They are depicted by Figure 5.403.1.
Figure 5.403.1. The two trees corresponding to the first example of the Example slot; each vertex contains the information where is the index of its father in the tree (by convention the father of the root is the root itself).
- All solutions
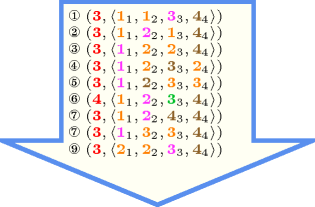
Figure 5.403.2 gives all solutions to the following non ground instance of the constraint: , , , , , .
Figure 5.403.2. All solutions corresponding to the non ground example of the constraint of the All solutions slot (the attribute is displayed as indices of the attribute)
- Typical
- Symmetry
Items of are permutable.
- Arg. properties
Functional dependency: determined by .
- Remark
Given a complete digraph of vertices as well as an unrestricted number of trees , the total number of solutions to the corresponding constraint corresponds to the sequence A000272 of the On-Line Encyclopaedia of Integer Sequences [Sloane10].
Extension of the constraint to the minimum spanning tree constraint is described in [DoomsKatriel06], [Regin08], [ReginRousseauRueherHoeve10].
- Algorithm
An arc-consistency filtering algorithm for the constraint is described in [BeldiceanuFlenerLorca05]. This algorithm is based on a necessary and sufficient condition that we now depict.
To any constraint we associate the digraph , where:
To each item of the collection corresponds a vertex of .
For every pair of items of the collection, where and are not necessarily distinct, there is an arc from to in if and only if is a potential value of .
A strongly connected component of is called a sink component if all the successors of all vertices of belong to . Let and respectively denote the number of sink components of and the number of vertices of with a loop.
The constraint has a solution if and only if:
Each sink component of contains at least one vertex with a loop,
The domain of has at least one value within interval .
Inspired by the idea of using dominators used in [ItalianoLauraSantaroni10] for getting a linear time algorithm for computing strong articulation points of a digraph , the worst case complexity of the algorithm proposed in [BeldiceanuFlenerLorca05] was also enhanced in a similar way by J.-G. Fages and X. Lorca [FagesLorca11].
- Reformulation
The constraint can be expressed in term of (1) a set of reified constraints for avoiding circuit between more than one node and of (2) reified constraints and of one sum constraint for counting the trees:
For each vertex of the collection we create a variable that takes its value within interval . This variable represents the rank of vertex within a solution. It is used to prevent the creation of circuit involving more than one vertex as explained now. For each pair of vertices of the collection we create a reified constraint of the form . The purpose of this constraint is to express the fact that, if there is an arc from vertex to another vertex , then should be strictly less than .
For each vertex of the collection we create a 0-1 variable and state the following reified constraint in order to force variable to be set to value 1 if and only if there is a loop on vertex . Finally we create a constraint for stating the fact that the number of trees is equal to the number of loops of the graph.
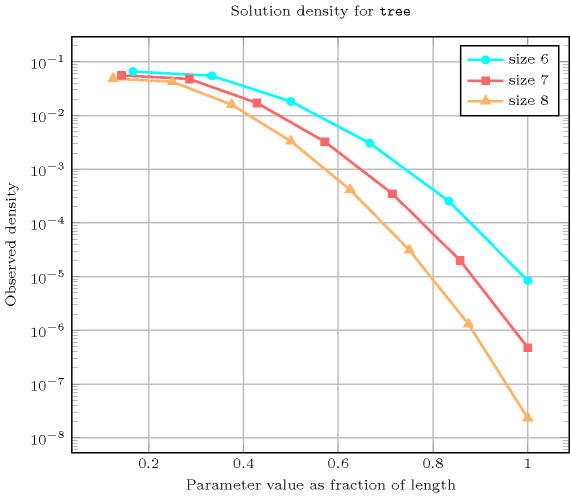
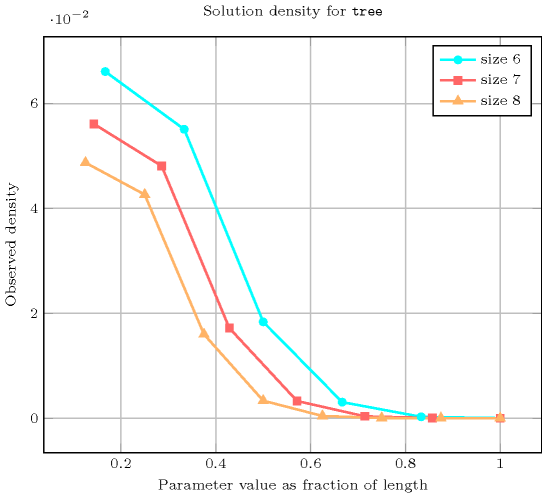
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 3 16 125 1296 16807 262144 4782969 Number of solutions for : domains
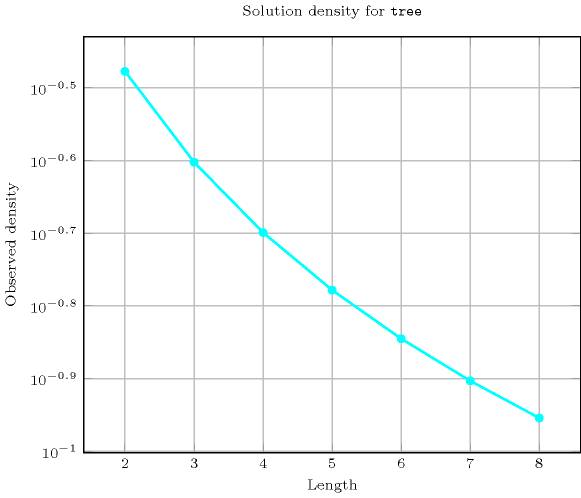
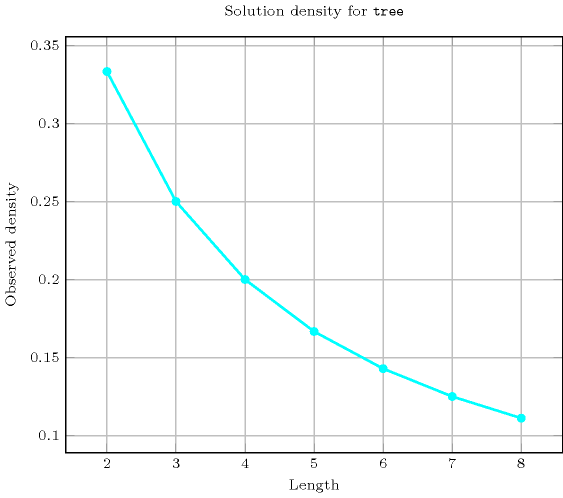
Length () 2 3 4 5 6 7 8 Total 3 16 125 1296 16807 262144 4782969 Parameter value 1 2 9 64 625 7776 117649 2097152 2 1 6 48 500 6480 100842 1835008 3 - 1 12 150 2160 36015 688128 4 - - 1 20 360 6860 143360 5 - - - 1 30 735 17920 6 - - - - 1 42 1344 7 - - - - - 1 56 8 - - - - - - 1 Solution count for : domains
- Systems
- See also
common keyword: , , (graph partitioning constraint), (connected component,tree).
implies (items to collection): .
related: (counting number of trees versus controlling how balanced the trees are), , (can be used for restricting number of children since discard loops associated with tree roots).
shift of concept: , , .
specialisation: (no limit on the number of children replaced by at most two children), (no limit on the number of children replaced by at most one child).
- Keywords
constraint type: graph constraint, graph partitioning constraint.
filtering: DFS-bottleneck, strong articulation point, arc-consistency.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
We use the graph property in order to specify the fact that the size of the largest strongly connected component should not exceed one. In fact each root of a tree is a strongly connected component with a single vertex. The second graph property enforces the number of trees to be equal to the number of connected components.
Parts (A) and (B) of Figure 5.403.3 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property, we display the two connected components of the final graph. Each of them corresponds to a tree. The constraint holds since all strongly connected components of the final graph have no more than one vertex and since .
Figure 5.403.3. Initial and final graph of the constraint
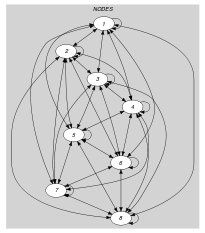
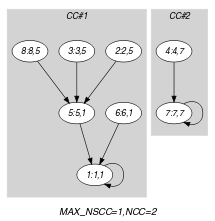
(a) (b)