5.407. two_layer_edge_crossing
| DESCRIPTION | LINKS | GRAPH |
- Origin
Inspired by [HararySchwenk72].
- Constraint
- Arguments
- Restrictions
- Purpose
is the number of line segments intersections.
- Example
-
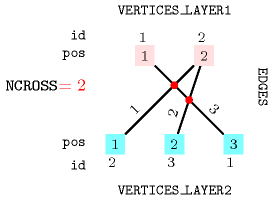
Figure 5.407.1 provides a picture of the example, where one can see the two line segments intersections. Each line segment of Figure 5.407.1 is labelled with its identifier and corresponds to an item of the collection. The two vertices on top of Figure 5.407.1 correspond to the items of the collection, while the three other vertices are associated with the items of .
Figure 5.407.1. Intersection between line segments joining two layers of the Example slot for the constraint
- Typical
- Symmetries
Arguments are permutable w.r.t. permutation .
Items of are permutable.
Items of are permutable.
- Arg. properties
Functional dependency: determined by , and .
- Remark
The two-layer edge crossing minimisation problem was proved to be NP-hard in [GareyJohnson83].
- See also
- Keywords
characteristic of a constraint: derived collection.
constraint arguments: pure functional dependency.
geometry: geometrical constraint, line segments intersection.
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
As usual for the two-layer edge crossing problem [HararySchwenk72], [DiBattistaEadesTamassiaTollis99], positions of the vertices on each layer are represented as a permutation of the vertices. We generate a derived collection that, for each edge, contains the position of its extremities on both layers. In the arc generator we use the restriction in order to generate a single arc for each pair of segments. This is required, since otherwise we would count more than once a line segments intersection.
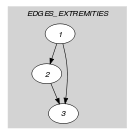
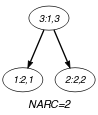
Parts (A) and (B) of Figure 5.407.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold.
Figure 5.407.2. Initial and final graph of the constraint
(a) (b)