3.7.188. Phi-tree
A constraint for which one of its filtering algorithms uses a balanced binary tree in order to efficiently evaluate the maximum or minimum value of a formula over all possible subsets of tasks of a given set of tasks . -trees were introduced by P. Vilím, first in the context of unary resources in [Vilim04] and in [Vilim07], and later on in the context of cumulative resources [Vilim09a], [Vilim09b]. Without loss of generality, let us sketch the main idea behind a -tree in the context of a cumulative resource of capacity . For this purpose we follow the description given in [Vilim09a]. Given a set of tasks where each task has an earliest possible start, a latest possible end, a duration and a resource consumption, assume we need to evaluate the earliest completion time over all tasks of under the hypothesis that we should not exceed the maximum resource capacity . Let us first introduce some notations:
denotes any non-empty subset of tasks of .
is the minimum over the earliest starts of the tasks in .
is the sum of the surfaces (i.e., the product of the duration by the resource consumption) of the tasks in .
Figure 3.7.51. Example of -tree associated with four tasks of respective duration and resource consumption , , , and of respective earliest start 1, 3, 8, 9 under the assumption that the maximum capacity of the cumulative resource is equal to 5
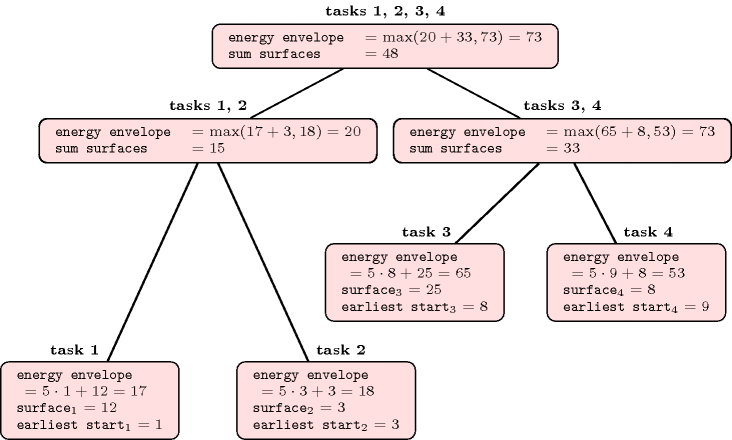
A common estimation of the earliest completion time over all tasks of is which can be rewritten as . The numerator of the last fraction is called the energy envelope of the set of tasks and the purpose of a -tree is to evaluate this quantity efficiently. For a node , let denote the set of leaves of the sub-tree rooted at . The leaves of the -tree correspond to the tasks of sorted from left to right by increasing earliest start. Each node of the -tree records both, the sum of the surfaces of the tasks in , as well as the energy envelope of the tasks in . The sum of the surfaces associated with a non-leave node of the tree corresponds to the sum of the surfaces of the children of , while the energy envelope of is equal to the maximum between on the one hand, the energy envelop of its right child and on the other hand the sum of the energy envelop of its left child and the recorded sum of surfaces of its right child (see [Vilim09a] for a justification of these recursive formulae). Figure 3.7.51 illustrates the construction of a -tree associated with four given tasks.