3.7.64. Convex hull relaxation
Given a non-convex set , is a convex outer approximation of if:
is convex,
If , then .
Given a non-convex set , is the convex hull of if:
is a convex outer approximation of ,
For every where is a convex outer approximation of , .
Part (A) of Figure 3.7.17 depicts a non-convex set, while part (B) gives its corresponding convex hull.
Figure 3.7.17. (B) Convex hull of a (A) non-convex set
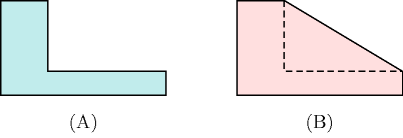
Within the context of linear programming the convex hull relaxation of a non-convex set corresponds to the set of linear constraints characterising the convex hull of .