3.7.109. Glue matrix
A reversible constraint for which the catalogue provides an automaton with counters and a glue matrix. A glue matrix is indexed by the states of the automaton associated with the considered constraint as well as by the states of the automaton associated with the reverse of the considered constraint. In the following we assume that the signature constraint involves consecutive variables of the sequence of variables of the reversible constraint (the signature constraint encodes the mapping of the sequence of variables of the constraint to symbols of the alphabet of the automaton). We consider a sequence of variables and a prefix and suffix of this sequence such that the prefix and suffix have variables in common. Let (resp. ) be the state of the automaton associated with the constraint (resp. the reverse constraint) upon reading the prefix (resp. the reverse of the suffix). The entry of the glue matrix corresponding to the state pair provides a function for computing the result associated with the sequence from the counters values associated with the prefix and the reverse suffix.
As an example consider the , which holds if is equal to the number of peaks of the sequence of variables . A peak corresponds to an increase between consecutive variables followed by a decrease between consecutive variables. Figure 3.7.32 gives the corresponding automaton that returns the number of peak of a sequence where, to each pair of consecutive variables corresponds a signature variable passed to the automaton. The following signature constraint links , and : .
Figure 3.7.32. Automaton of the constraint and its glue matrix
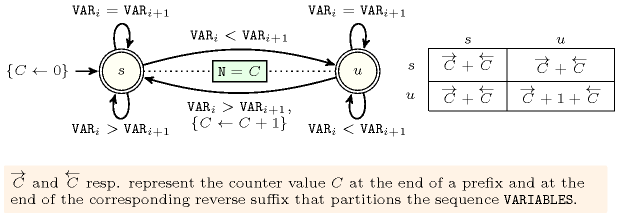
Figure 3.7.33 illustrates the use of the glue matrix of the constraint on the sequence decomposed in a prefix and a suffix that overlap by one position, one position since the arity of the signature constraint is equal to two. Since the automaton of the constraint ends up in state when applied to the prefix and to the reverse suffix we use the lower rightmost entry of the glue matrix to link the total number of peaks of the sequence with the number of peaks of the prefix and the suffix .
Figure 3.7.33. Illustrating the use of the state pair of the glue matrix for linking with the counters variables obtained after reading the prefix and corresponding suffix of the sequence ; note that the suffix (in pink) is proceed in reverse order; the left (resp. right) table shows the initialisation (for ) and the evolution (for ) of the state of the automaton and of its counter upon reading the prefix (resp. the suffix ).
