3.7.172. Open automaton constraint

A constraint for which the set of solutions can be recognised by a so called open automaton. An open automaton is a finite deterministic automaton taking as input a sequence of variables V 1 V 2 β‹―V n as well as a sequence of 0-1 variables B 1 B 2 β‹―B n . A variable B i (1≀i≀n) set to value 0 means that the corresponding variable V i is removed from the sequence of variables V 1 V 2 β‹―V n .

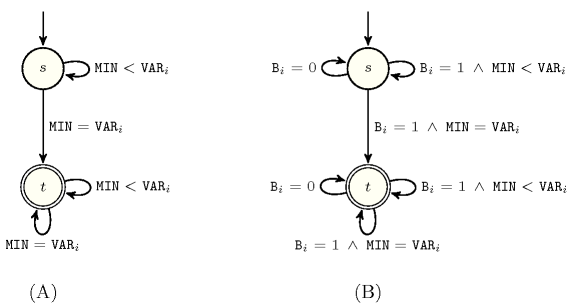
Consider a constraint π’ž for which we already have a finite deterministic automaton π’œ that only accepts the set of solutions of π’ž. Constructing the finite deterministic automaton π’œ ' that only recognises the set of solutions to the open version of constraint C can be done in a systematic way from the automaton π’œ. First, to each transition of π’œ we add the fact that the corresponding Boolean variable must also be equal to 1. Second, to each state of π’œ we add a loop transition for which the corresponding Boolean variable B i (1≀i≀n) must be equal to 0 (since variable V i is ignored, we stay within the same state). FigureΒ 3.7.45 illustrates this construction in the context of the πš–πš’πš—πš’πš–πšžπš– constraint and of its open counterpart, the πš˜πš™πšŽπš—_πš–πš’πš—πš’πš–πšžπš– constraint.

Figure 3.7.45. Constructing the (B)Β automaton of the πš˜πš™πšŽπš—_πš–πš’πš—πš’πš–πšžπš–(𝙼𝙸𝙽,βŒ©πš…π™°πš 1 𝙱 1 ,πš…π™°πš 2 𝙱 2 ,β‹―,πš…π™°πš n 𝙱 n βŒͺ) constraint from the (A)Β automaton of the πš–πš’πš—πš’πš–πšžπš–(𝙼𝙸𝙽,βŒ©πš…π™°πš 1 ,πš…π™°πš 2 ,β‹―,πš…π™°πš n βŒͺ) constraint
ctrs/preface-185-tikz