3.7.214. Reverse of a constraint
A constraint which has a reverse constraint, where the reverse is defined in the following way. Consider two constraints and for which, in both cases, the argument is a collection of items that functionally determines all the other arguments .
The constraint is the reverse constraint of constraint if, for any collection of items , we have the equivalence , where denotes the collection where the items of the collection are reversed. When constraints and are identical we say that constraint is its own reverse.
The previous enumeration provides the list of reversible constraints where, for each reversible constraint, we give its reverse only when it is different from the original constraint.
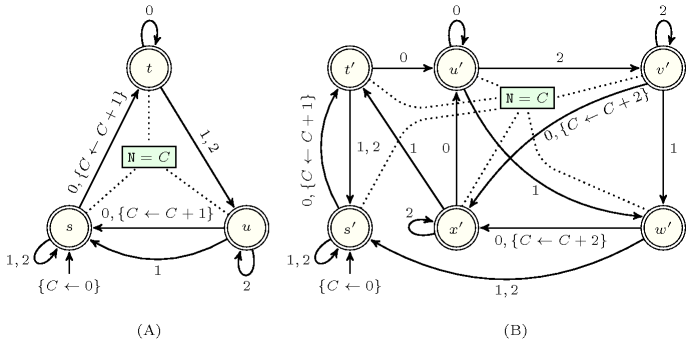
Note that if a constraint can be represented by a counter deterministic automaton with one single counter that is only incremented and for which all states are accepting, then by computing the reverse automaton, the corresponding reverse constraint can be mechanically obtained. However note that the reverse automaton may be non-deterministic and may contain transitions [Mohri2009]. Figure 3.7.57 gives an automaton counting the number of occurrences of words 001 in a sequence and its reverse automaton. Figure 3.7.58 provides an automaton with one counter and its reverse automaton that has a different number of states.
Figure 3.7.57. (A) Counter automaton returning the number of occurrences of word 001 in a sequence, and (B) its reverse counter automaton (returning the number of occurrences of word 100 in a sequence)
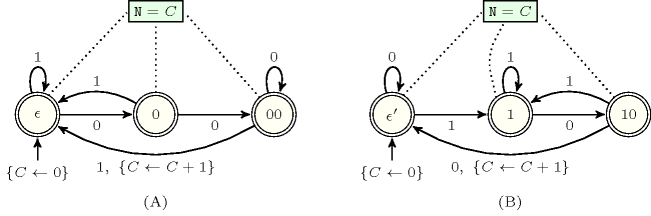
Figure 3.7.58. (A) Counter automaton, and (B) its reverse counter automaton which has a different number of states