3.7.252. Sweep
A constraint for which the filtering algorithm may use a sweep algorithm. A sweep algorithm [PreparataShamos85] solves a problem by moving an imaginary object (usually a line, a plane or sometime a point). The object does not move continuously, but only at particular points where we actually do something. A sweep algorithm uses the following two data structures:
A data structure called the sweep status, which contains information related to the current position of the object that moves,
A data structure named the event point series, which holds the events to process.
The algorithm initialises the sweep status for the initial position of the imaginary object. Then the object jumps from one event to the next event; each event is handled by updating the status of the sweep.
A first typical application reported in [BeldiceanuCarlsson01sweep] of the idea of sweep within the context of constraint programming is to aggregate several constraints that have two variables in common in order to perform more deduction. Let:
and be two distinct variables,
be a set of constraints such that all constraints mention and .
The sweep algorithm tries to adjust the minimum value of with respect to the conjunction of the previous constraints by moving a sweep-line from the minimum value of to its maximum value. It accumulates within the sweep-line status the values to be currently removed from the domain of . If, for the current position of the sweep-line, all values of have to be removed, then the algorithm removes value from the domain of . The events to process correspond to the starts and ends of forbidden two-dimensional regions with respect to constraints and variables and . Forbidden regions are a way to represent constraints that is suited for this sweep algorithm. A forbidden region of the constraint with respect to the variables and is an ordered pair of intervals such that: has no solution in which and .
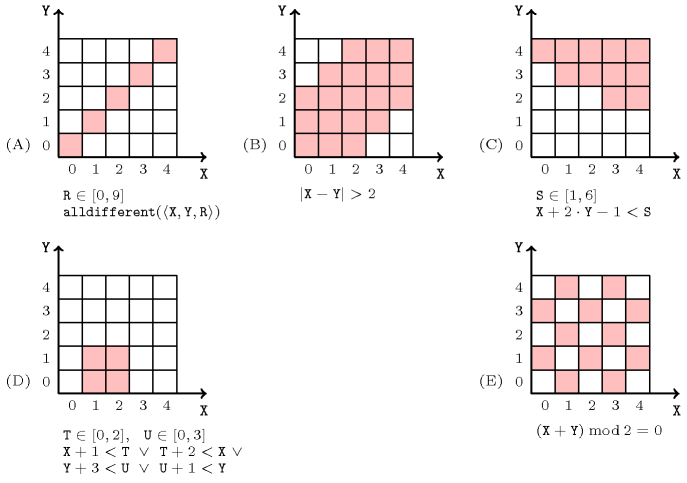
Figure 3.7.78 shows five constraints and their respective forbidden regions (in pink) with respect to two given variables and and their domains. The first constraint requires that , and be pairwise distinct. Constraints (B,C) are usual arithmetic constraints.Within the context of continuous variables, Chabertet al. [ChabertBeldiceanu10] shows how to compute a forbidden region that contains a given unfeasible point for numerical constraints with arbitrary mathematical expressions. Constraint (D) can be interpreted as requiring that two rectangles of respective origins and and sizes and do not overlap. Finally, constraint (E) is a parity constraint of the sum of and .
Figure 3.7.78. Examples of forbidden regions (in pink) according to the two variables and (, ) for five constraints
We illustrate the use of the sweep algorithm on a concrete example. Assume that we want to find out the minimum value of variable with respect to the conjunction of the five constraints that were introduced by Figure 3.7.78, that is versus the following conjunction of constraints:
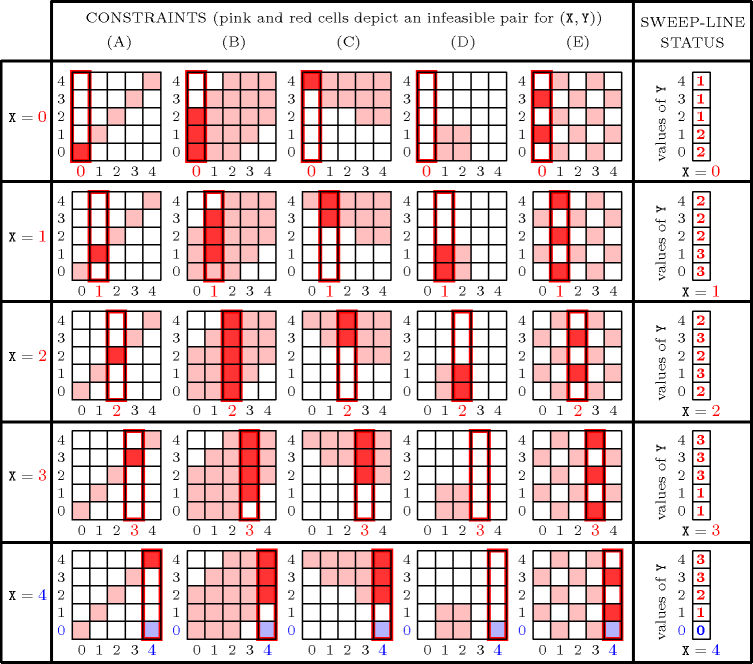
Figure 3.7.79 shows the content of the sweep-line status (i.e., the forbidden values for according the current position of the sweep-line) for different positions of the sweep-line. More precisely, the sweep-line status can be viewed as an array (see the rightmost part of Figure 3.7.79) which records for each possible value of the number of forbidden regions that currently intersect the sweep-line (see the leftmost part of Figure 3.7.79 where these forbidden regions are coloured in red). The smallest possible value of is 4, since this is the first position of the sweep-line where the sweep-line status contains a value of which is not forbidden (i.e., , is not covered by any forbidden region).
Figure 3.7.79. Sweep-line status while sweeping through the potential values of variable (i.e., values from 0 to 4) until a potentially feasible point , wrt the five constraints (A), (B), (C), (D) and (E) is found; the sweep-line status (i.e., the rightmost column) records for a potential value of variable and for each potential value of variable how many constraints are violated when both and .
A second similar application of the idea of sweep in the context of the cardinality operator [VanHentenryckDeville91], where all constraints have at least two variables in common, is reported in [BeldiceanuCarlssonSoftSweep01]. As before, each constraint of the cardinality operator is defined by its forbidden regions with respect to a pair of variables that occur in every constraint. In addition to that, a constraint is also defined by its safe regions, where a safe region is the set of assignments to the pair located in a rectangle such that the constraint always holds, no matter which values are taken by the other variables of . Then the extended sweep algorithm filters the pair of variables right from the beginning according to the minimum and maximum number of constraints of the cardinality operator that have to hold.
A third typical application reported in [BeldiceanuCarlssonPoderSadekTruchet07] and in [CarlssonBeldiceanuMartin08] of the idea of sweep within the context of multi-dimensional placement problems (see for instance the and the constraints) for filtering each coordinate of the origin of an object to place is as follows. To adjust the minimum (respectively maximum) value of a coordinate of the origin we perform a recursive traversal of the placement space in increasing (respectively decreasing) lexicographic order and skips infeasible points that are located in a multi-dimensional forbidden set. Each multi-dimensional forbidden set is computed from a constraint where object occurs (for instance a non-overlapping constraint in the context of the and the constraints).