Global Constraint Catalog

2.3.2.4. Graph properties

We represent a global constraint as the search of a subgraph (i.e., a final graph) of a known initial graph, so that this final graph satisfies a given set of graph properties and possibly belongs to a specific graph class. Most graph properties have the form $𝙿𝚊𝚛𝚊𝚖𝚎𝚝𝚎𝚛 𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗 𝙴𝚡𝚙$ or the form $𝙿𝚊𝚛𝚊𝚖𝚎𝚝𝚎𝚛 \notin [{𝙴𝚡𝚙}_{1}, {𝙴𝚡𝚙}_{2}]$ , where $𝙿𝚊𝚛𝚊𝚖𝚎𝚝𝚎𝚛$ is a graph parameter [Berge70], [GondranMinoux84], $𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗$ is one of the comparison operators $=$ , $<$ , $\geq$ , $>$ , $\leq$ , $\neq$ , and $𝙴𝚡𝚙$ , ${𝙴𝚡𝚙}_{1}$ , ${𝙴𝚡𝚙}_{2}$ are expressions that can be evaluated to an integer. Before defining each graph parameter, let's first introduce some basic vocabulary on graphs.

Graph terminology and notations

A digraph $G = (V (G), E (G))$ is a pair where $V (G)$ is a finite set, called the set of vertices, and where $E (G)$ is a set of ordered pairs of vertices, called the set of arcs. The arc, path, circuit and strongly connected component of a graph $G$ correspond to oriented concepts, while the edge, chain, cycle and connected component are non-oriented concepts. However, as reported in [Berge70] an undirected graph can be seen as a digraph where to each edge we associate the corresponding two arcs. Parts (A) and (B) of Figure 2.3.5 respectively illustrate the terms for undirected graphs and digraphs.

Figure 2.3.5. Graph terminology for an undirected graph and a digraph (similar concepts are outlined with the same colour)

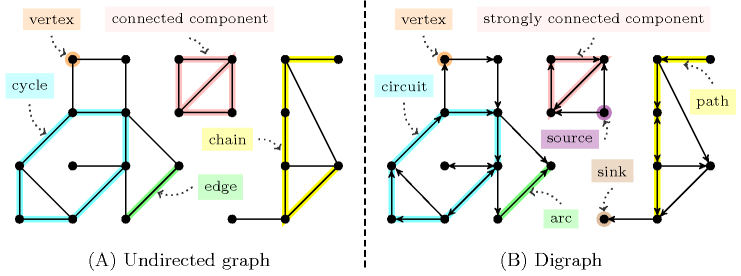
We say that $e_{2}$ is a successor of $e_{1}$ if there exists an arc that starts from $e_{1}$ and ends at $e_{2}$ . In the same way, we say that $e_{2}$ is a predecessor of $e_{1}$ if there exists an arc that starts from $e_{2}$ and ends at $e_{1}$ .
A vertex of $G$ that does not have any predecessor is called a source. A vertex of $G$ that does not have any successor is called a sink.
A sequence $(e_{1}, e_{2}, \dots, e_{k})$ of edges of $G$ such that each edge has a common vertex with the previous edge, and the other vertex common to the next edge is called a chain of length $k$ . A chain where all vertices are distinct is called an elementary chain. Each equivalence class of the relation “ $e_{i}$ is equal to $e_{j}$ or there exists a chain between $e_{i}$ and $e_{j}$ ” is a connected component of the graph $G$ .
A sequence $(e_{1}, e_{2}, \dots, e_{k})$ of arcs of $G$ such that, for each arc $e_{i}$ $(1 \leq i < k)$ the end of $e_{i}$ is equal to the start of the arc $e_{i + 1}$ , is called a path of length $k$ . A path where all vertices are distinct is called an elementary path. Each equivalence class of the relation “ $e_{i}$ is equal to $e_{j}$ or there exists a path between $e_{i}$ and $e_{j}$ ” is a strongly connected component of the graph $G$ .
A chain $(e_{1}, e_{2}, \dots, e_{k})$ of $G$ is called a cycle if the same edge does not occur more than once in the chain and if the two extremities of the chain coincide. A cycle $(e_{1}, e_{2}, \dots, e_{k})$ of $G$ is called a circuit if for each edge $e_{i}$ $(1 \leq i < k)$ , the end of $e_{i}$ is equal to the start of the edge $e_{i + 1}$ .
Given a graph $G$ , we define the reduced graph $R (G)$ of $G$ as follows: to each strongly connected component of $G$ corresponds a vertex of $R (G)$ ; to each arc of $G$ that connects different strongly connected components corresponds an arc in $R (G)$ (multiple arcs between the same pair of vertices are merged).
The rank function associated with the vertices $V (G)$ of a graph $G$ that does not contain any circuit is defined in the following way:
- The rank of the vertices that do not have any predecessor (i.e., the sources) is equal to 0,
- The rank $r$ of a vertex $v$ that is not a source is the length of longest path $(e_{1},$ $e_{2},$ $\dots,$ $e_{r})$ such that the start of the arc $e_{1}$ is a source and the end of arc $e_{r}$ is the vertex $v$ .

We now present the different notations used in the catalogue:

$[k]$ corresponds to ${1, \dots, k}$ for $k$ any positive integer.
Given a set $X$ , $| X |$ is the number of its elements.
Given two sets $X$ and $Y$ , $X ⊎ Y$ denotes the union of the two sets when they are disjoint.
Given a digraph $G$ and $x \in V (G)$ , $d_{G}^{+} (x) = | {y : y \in V (G) : (x, y) \in E (G)} |$ and $d_{G}^{-} (x) = | {y : y \in V (G) : (y, x) \in E (G)} |$ .
Given a digraph $G$ and $X$ a subset of $V (G)$ , the sub-digraph of $G$ induced by $X$ is the digraph $G [X]$ where $V (G [X]) = X$ and $E (G [X]) = X^{2} \cap E (G)$ . By aim of simplicity, we denote $G [V (G) - X]$ by $G - X$ . Moreover, if $X = {x}$ , we use $G - x$ instead of $G - {x}$ .
Given two digraph $G_{1}$ and $G_{2}$ such that $V (G_{1}) \cap V (G_{2}) = \emptyset$ , $G_{1} \oplus G_{2}$ denotes the graph whose vertices set is $V (G_{1}) \cup V (G_{2})$ and whose arcs set is $E (G_{1}) \cup E (G_{2})$ .
Given a graph parameter $𝐏 \in {𝐍𝐂𝐂, 𝐍𝐒𝐂𝐂}$ , a digraph $G$ and an integer $k$ , $𝐂𝐇 (G, k)$ is the number of connected components (respectively strongly connected components) of $G$ with cardinal $k$ .

Given a graph parameter, for instance the number of connected components, ${𝐍𝐂𝐂}_{𝙸𝙽𝙸𝚃𝙸𝙰𝙻}$ will denote the number of connected components of the initial graph (i.e., the graph induced by the constraint under consideration), $𝐍𝐂𝐂$ will denote the number of connected components of the final graph (i.e., a subgraph of the initial graph). The use of $𝐍𝐂𝐂 (G)$ will denote the number of connected components of the digraph $G$ .

Given a global constraint $C$ , and a graph parameter $𝐏$ used in the description of $C$ , $\underset{̲}{𝐏}$ (respectively $\bar{𝐏}$ ) denotes a lower bound (respectively upper bound) of $𝐏$ among all possible final graphs compatible with the current status of $C$ .

Graph parameters

We list in alphabetic order the different graph parameters we consider for a final graph $G_{f} = (V (G_{f}), E (G_{f}))$ associated with a global constraint and give an example of constraint where they are used:

$𝐌𝐀𝐗_𝐃𝐑𝐆$ : largest distance between sources and sinks in the reduced graph associated with $G_{f}$ (adjacent vertices are at a distance of 1).

EXAMPLE: We do not provide any example since $𝐌𝐀𝐗_𝐃𝐑𝐆$ is currently not used.
$𝐌𝐀𝐗_𝐈𝐃$ : number of predecessors of the vertex of $G_{f}$ that has the maximum number of predecessors without counting an arc from a vertex to itself.

EXAMPLE: The $𝚌𝚒𝚛𝚌𝚞𝚒𝚝$ constraint uses the graph property $𝐌𝐀𝐗_𝐈𝐃 = 1$ in order to force each vertex of the final graph to have at most one predecessor.
$𝐌𝐀𝐗_𝐍𝐂𝐂$ : number of vertices of the largest connected component of $G_{f}$ .

EXAMPLE: The $𝚕𝚘𝚗𝚐𝚎𝚜𝚝_𝚌𝚑𝚊𝚗𝚐𝚎$ $(𝚂𝙸𝚉𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁)$ constraint uses the graph property $𝐌𝐀𝐗_𝐍𝐂𝐂 = 𝚂𝙸𝚉𝙴$ in order to catch in $𝚂𝙸𝚉𝙴$ the maximum number of consecutive variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection for which constraint $𝙲𝚃𝚁$ holds.
$𝐌𝐀𝐗_𝐍𝐒𝐂𝐂$ : number of vertices of the largest strongly connected component of $G_{f}$ .

EXAMPLE: The $𝚝𝚛𝚎𝚎$ constraint covers a digraph by a set of trees in such a way that each vertex belongs to a distinct tree. It uses the graph-property $𝐌𝐀𝐗_𝐍𝐒𝐂𝐂$ $\leq$ 1 in order to avoid to have any circuit involving more than one vertex.
$𝐌𝐀𝐗_𝐎𝐃$ : number of successors of the vertex of $G_{f}$ that has the maximum number of successors without counting an arc from a vertex to itself.

EXAMPLE: The $𝚝𝚘𝚞𝚛$ constraint forces to cover a graph with a Hamiltonian cycle. It uses the graph-property $𝐌𝐀𝐗_𝐎𝐃 = 2$ to enforce that each vertex of $G_{f}$ have at most twoSince the $𝚝𝚘𝚞𝚛$ constraint uses the $𝐶𝐿𝐼𝑄𝑈𝐸 (\neq)$ arc generator the vertices of $G_{f}$ do not have any loop. successors.
$𝐌𝐈𝐍_𝐃𝐑𝐆$ : smallest distance between sources and sinks in the reduced graph associated with $G_{f}$ (adjacent vertices are at a distance of 1).

EXAMPLE: We do not provide any example since $𝐌𝐈𝐍_𝐃𝐑𝐆$ is currently not used by any constraint.
$𝐌𝐈𝐍_𝐈𝐃$ : number of predecessors of the vertex of $G_{f}$ that has the minimum number of predecessors without counting an arc from a vertex to itself.

EXAMPLE: The $𝚝𝚘𝚞𝚛$ constraint forces to cover a graph with a Hamiltonian cycle. It uses the graph-property $𝐌𝐈𝐍_𝐈𝐃 = 2$ to enforce that each vertex of $G_{f}$ have at most twoSince the $𝚝𝚘𝚞𝚛$ constraint uses the $𝐶𝐿𝐼𝑄𝑈𝐸 (\neq)$ arc generator the vertices of $G_{f}$ do not have any loop. predecessors.
$𝐌𝐈𝐍_𝐍𝐂𝐂$ : number of vertices of the smallest connected component of $G_{f}$ .

EXAMPLE: Within the $𝚐𝚛𝚘𝚞𝚙$ constraint, each connected component of $G_{f}$ corresponds to a maximum sequence of consecutive variables that take their values in a given set of values. Therefore, the graph-property $𝐌𝐈𝐍_𝐍𝐂𝐂 = 𝙼𝙸𝙽_𝚂𝙸𝚉𝙴$ forces that the smallest sequence of such variables consist of $𝙼𝙸𝙽_𝚂𝙸𝚉𝙴$ variables.
$𝐌𝐈𝐍_𝐍𝐒𝐂𝐂$ : number of vertices of the smallest strongly connected component of $G_{f}$ .

EXAMPLE: The $𝚌𝚒𝚛𝚌𝚞𝚒𝚝$ $(N O D E S)$ constraint forces covering a digraph with one circuit visiting once all its vertices. The graph-property $𝐌𝐈𝐍_𝐍𝐒𝐂𝐂 = | 𝙽𝙾𝙳𝙴𝚂 |$ forces that the smallest strongly connected component of $G_{f}$ contain $| 𝙽𝙾𝙳𝙴𝚂 |$ vertices. Since $| 𝙽𝙾𝙳𝙴𝚂 |$ also corresponds to the number of vertices of the initial graph this means that $G_{f}$ is a strongly connected component involving all the vertices. This is clearly a necessary conditionOf course, this is not enough, and the description of the $𝚌𝚒𝚛𝚌𝚞𝚒𝚝$ constraint asks for some other properties. for having a circuit visiting once all vertices.
$𝐌𝐈𝐍_𝐎𝐃$ : number of successors of the vertex of $G_{f}$ that has the minimum number of successors without counting an arc from a vertex to itself.

EXAMPLE: The $𝚝𝚘𝚞𝚛$ constraint forces to cover a graph with a Hamiltonian cycle. It uses the graph-property $𝐌𝐈𝐍_𝐎𝐃 = 2$ to enforce that each vertex of $G_{f}$ have at most twoSince the $𝚝𝚘𝚞𝚛$ constraint uses the $𝐶𝐿𝐼𝑄𝑈𝐸 (\neq)$ arc generator the vertices of $G_{f}$ do not have any loop. successors.
$𝐍𝐀𝐑𝐂$ : cardinality of the set $E (G_{f})$ .

EXAMPLE: The $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ constraint forces that each variable of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ take a value that is distinct from all the values assigned to the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .

This is imposed by creating an arc from each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ to each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ . To each arc corresponds an equality constraint involving the variables associated with the extremities of the arc. Finally, the graph property $𝐍𝐀𝐑𝐂 = 0$ forces $G_{f}$ to be empty so that no value is both assigned to a variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ as well as to a variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .
$𝐍𝐀𝐑𝐂_𝐍𝐎_𝐋𝐎𝐎𝐏$ : cardinality of the set $E (G_{f})$ without considering the arcs linking the same vertex (i.e., a loop).

EXAMPLE: The constraint $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚜𝚊𝚖𝚎_𝚟𝚊𝚕𝚞𝚎$ uses the $𝐍𝐀𝐑𝐂_𝐍𝐎_𝐋𝐎𝐎𝐏$ graph-property.
$𝐍𝐂𝐂$ : number of connected components of $G_{f}$ .

EXAMPLE: The $𝚝𝚛𝚎𝚎$ constraint covers a digraph by $𝙽𝚃𝚁𝙴𝙴𝚂$ trees in such a way that each vertex belongs to a distinct tree. It uses the graph-property $𝐍𝐂𝐂 = 𝙽𝚃𝚁𝙴𝙴𝚂$ in order to state that $G_{f}$ is made up from $𝙽𝚃𝚁𝙴𝙴𝚂$ connected components.
$𝐍𝐒𝐂𝐂$ : number of strongly connected components of $G_{f}$ .

EXAMPLE: The constraint $𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ forces $𝙽𝚅𝙰𝙻$ to be equal to the number of distinct values assigned to the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . This is enforced by using the graph-property $𝐍𝐒𝐂𝐂 = 𝙽𝚅𝙰𝙻$ . Each strongly connected component of the final graph corresponds to the variables that are assigned to the same value.
$𝐍𝐒𝐈𝐍𝐊$ : number of vertices of $G_{f}$ that do not have any successor.

EXAMPLE: The $𝚜𝚊𝚖𝚎$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ forces that the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ collection correspond to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collection according to a permutation.

We first create an arc from each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ to each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ . To each arc corresponds an equality constraint involving the variables associated with the extremities of the arc. We use the graph-property $𝐍𝐒𝐈𝐍𝐊 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ in order to express the fact that each value assigned to a variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ should also be assigned to a variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .
$𝐍𝐒𝐈𝐍𝐊_𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ : sum over the different connected components of $G_{f}$ of the minimum of the number of sinks and the number of sources of a connected component.

EXAMPLE: The $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚟𝚊𝚛$ $(𝙲, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ constraint forces $𝙲$ to be the minimum number of values to change in the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections of variablesBoth collections have the same number of variables., so that the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ correspond to the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ according to a permutation.

A connected component $𝒞_{𝑣𝑎𝑙}$ of the final graph $G_{f}$ corresponds to all variables that are assigned to the same value $𝑣𝑎𝑙$ : the sources and the sinks of $𝒞_{𝑣𝑎𝑙}$ respectively correspond to the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and to the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ that are assigned to $𝑣𝑎𝑙$ . For a connected component, the minimum of the number of sources and sinks expresses the number of variables for which we do not need to make any change. Therefore we use the graph-property $𝐍𝐒𝐈𝐍𝐊_𝐍𝐒𝐎𝐔𝐑𝐂𝐄 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | - 𝙲$ for encoding the meaning of the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚟𝚊𝚛$ constraint.
$𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ : number of vertices of $G_{f}$ that do not have any predecessor.

EXAMPLE: The $𝚜𝚊𝚖𝚎$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ forces that the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ collection correspond to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collection according to a permutation.

We first create an arc from each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ to each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ . To each arc corresponds an equality constraint involving the variables associated with the extremities of the arc. We use the graph-property $𝐍𝐒𝐎𝐔𝐑𝐂𝐄 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |$ in order to express the fact that each value assigned to a variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ should also be assigned to a variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .
$𝐍𝐓𝐑𝐄𝐄$ : number of vertices of $G_{f}$ that do not belong to any circuit and for which at least one successor belongs to a circuit. Such vertices can be interpreted as root nodes of a tree.

EXAMPLE: The $𝚌𝚢𝚌𝚕𝚎$ $(𝙽𝙲𝚈𝙲𝙻𝙴, 𝙽𝙾𝙳𝙴𝚂)$ forces that $𝙽𝙲𝚈𝙲𝙻𝙴$ equal the number of circuits for covering an initial graph in such a way that each vertex belongs to a single circuit.

The graph-property $𝐍𝐓𝐑𝐄𝐄 = 0$ forces that all vertices of the final graph belong to a circuit.
$𝐍𝐕𝐄𝐑𝐓𝐄𝐗$ : cardinality of the set $V (G_{f})$ .

EXAMPLE: The $𝚌𝚞𝚝𝚜𝚎𝚝$ $(𝚂𝙸𝚉𝙴_𝙲𝚄𝚃𝚂𝙴𝚃, 𝙽𝙾𝙳𝙴𝚂)$ constraint considers a digraph with $n$ vertices described by the $𝙽𝙾𝙳𝙴𝚂$ collection. It forces that the subset of kept vertices of cardinality $n - 𝚂𝙸𝚉𝙴_𝙲𝚄𝚃𝚂𝙴𝚃$ and their corresponding arcs form a graph without a circuit. It uses the graph-property $𝐍𝐕𝐄𝐑𝐓𝐄𝐗 = n - 𝚂𝙸𝚉𝙴_𝙲𝚄𝚃𝚂𝙴𝚃$ for enforcing that the final graph $G_{f}$ contain the required number of vertices.
$𝐑𝐀𝐍𝐆𝐄_𝐃𝐑𝐆$ : difference between the largest distance between sources and sinks in the reduced graph associated with $G_{f}$ and the smallest distance between sources and sinks in the reduced graph associated with $G_{f}$ .

EXAMPLE: The $𝚝𝚛𝚎𝚎_𝚛𝚊𝚗𝚐𝚎$ constraint forces to cover a digraph in such a way that each vertex belongs to a distinct tree. In addition it forces the difference between the longest and the shortest paths of $G_{f}$ to be equal to the variable $𝚁$ . For this purpose it uses the graph-property $𝐑𝐀𝐍𝐆𝐄_𝐃𝐑𝐆 = 𝚁$ .
$𝐑𝐀𝐍𝐆𝐄_𝐍𝐂𝐂$ : difference between the number of vertices of the largest connected component of $G_{f}$ and the number of vertices of the smallest connected component of $G_{f}$ .

EXAMPLE: We do not provide any example since $𝐑𝐀𝐍𝐆𝐄_𝐍𝐂𝐂$ is currently not used by any constraint.
$𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂$ : difference between the number of vertices of the largest strongly connected component of $G_{f}$ and the number of vertices of the smallest strongly connected component of $G_{f}$ .

EXAMPLE: The $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ $(𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ constraint forces $𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ to be equal to the difference between the number of occurrences of the value that occurs the most and the value that occurs the least within the collection of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . Each strongly connected component of $G_{f}$ corresponds to the variables that are assigned to the same value. The graph property $𝐑𝐀𝐍𝐆𝐄_𝐍𝐒𝐂𝐂 = 𝙱𝙰𝙻𝙰𝙽𝙲𝙴$ allows for expressing this definition.
$𝐎𝐑𝐃𝐄𝐑 (𝚛𝚊𝚗𝚔, 𝚍𝚎𝚏𝚊𝚞𝚕𝚝, 𝚊𝚝𝚝𝚛)$
- $𝚛𝚊𝚗𝚔$ is an integer or an argument of type integer of the global constraint,
- $𝚍𝚎𝚏𝚊𝚞𝚕𝚝$ is an integer,
- $𝚊𝚝𝚝𝚛$ is an attribute corresponding to an integer or to a domain variable that occurs in all the collections that were used for generating the vertices of the initial graph.
We explain what is the value associated with $𝐎𝐑𝐃𝐄𝐑 (𝚛𝚊𝚗𝚔, 𝚍𝚎𝚏𝚊𝚞𝚕𝚝, 𝚊𝚝𝚝𝚛)$ . Let $𝒱$ denote the vertices of rank $𝚛𝚊𝚗𝚔$ of $G_{f}$ from which we remove any loops.
- When $𝒱$ is not empty, it corresponds to the values of attribute $𝚊𝚝𝚝𝚛$ of the items associated with the vertices of $𝒱$ ,
- Otherwise, when $𝒱$ is empty, it corresponds to the default value $𝚍𝚎𝚏𝚊𝚞𝚕𝚝$ .
EXAMPLE: The $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ forces $𝙼𝙸𝙽$ to be the minimum value of the collection of domain variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . There is an arc from a variable ${𝚟𝚊𝚛}_{1}$ to a variable ${𝚟𝚊𝚛}_{2}$ if and only if ${𝚟𝚊𝚛}_{1} < {𝚟𝚊𝚛}_{2}$ . The graph-property $𝐎𝐑𝐃𝐄𝐑 (0, 𝙼𝙰𝚇𝙸𝙽𝚃, 𝚟𝚊𝚛) = 𝙼𝙸𝙽$ expresses the fact that $𝙼𝙸𝙽$ is equal to the value of the source of $G_{f}$ (since $𝚛𝚊𝚗𝚔 = 0$ ).
$𝐏𝐀𝐓𝐇_𝐅𝐑𝐎𝐌_𝐓𝐎 (𝚊𝚝𝚝𝚛, 𝚏𝚛𝚘𝚖, 𝚝𝚘)$
- - $𝚊𝚝𝚝𝚛$ is an attribute corresponding to an integer that occurs in all the collections that were used for generating the vertices of the initial graph,
  - $𝚏𝚛𝚘𝚖$ is an integer or an argument of type integer of the global constraint,
  - $𝚝𝚘$ is an integer or an argument of type integer of the global constraint.
  Let $ℱ$ (respectively $𝒯$ ) denote the vertices of $G_{f}$ such that $𝚊𝚝𝚝𝚛$ is equal to $𝚏𝚛𝚘𝚖$ (respectively $𝚝𝚘$ ). $𝐏𝐀𝐓𝐇_𝐅𝐑𝐎𝐌_𝐓𝐎 (𝚊𝚝𝚝𝚛, 𝚏𝚛𝚘𝚖, 𝚝𝚘)$ is equal to 1 if there exists a path between each vertex of $ℱ$ and each vertex of $𝒯$ , and 0 if there exists no path between a vertex of $ℱ$ and a vertex of $𝒯$ .
- - $𝚊𝚝𝚝𝚛$ is an attribute corresponding to an integer that occurs in all the collections that were used for generating the vertices of the initial graph,
  - $𝚏𝚛𝚘𝚖$ is an attribute corresponding to an integer or to a set of integers that occurs in all the collections that were used for generating the vertices of the initial graph,
  - $𝚝𝚘$ is an attribute corresponding to an integer or to a set of integers that occurs in all the collections that were used for generating the vertices of the initial graph,
  For each vertex $v$ of $G_{f}$ let:
  - $ℱ_{v}$ the set of vertices for which the value of the attribute $𝚊𝚝𝚝𝚛$ is equal to the $𝚏𝚛𝚘𝚖$ attribute (or is included within the $𝚏𝚛𝚘𝚖$ attribute when it corresponds to a set of integers).
  - $𝒯_{v}$ the set of vertices for which the value of the attribute $𝚊𝚝𝚝𝚛$ is equal to the $𝚝𝚘$ attribute (or is included within the $𝚝𝚘$ attribute when it corresponds to a set of integers).
  $𝐏𝐀𝐓𝐇_𝐅𝐑𝐎𝐌_𝐓𝐎 (𝚊𝚝𝚝𝚛, 𝚏𝚛𝚘𝚖, 𝚝𝚘)$ is equal to
  - 1 if for each vertex of $G_{f}$ there exists a path between each vertex of $ℱ_{v}$ and each vertex of $𝒯_{v}$ .
  - 0 if for a vertex of $G_{f}$ there is no path between a vertex of $ℱ_{v}$ and a vertex of $𝒯_{v}$ .
EXAMPLE: The constraints $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜𝚎𝚚$ and $𝚜𝚝𝚊𝚋𝚕𝚎_𝚌𝚘𝚖𝚙𝚊𝚝𝚒𝚋𝚒𝚕𝚒𝚝𝚢$ use the $𝐏𝐀𝐓𝐇_𝐅𝐑𝐎𝐌_𝐓𝐎$ graph-property.
$𝐏𝐑𝐎𝐃 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$
- $𝚌𝚘𝚕$ is a collection that was used for generating the vertices of the initial graph,
- $𝚊𝚝𝚝𝚛$ is an attribute corresponding to an integer or to a domain variable of the collection $𝚌𝚘𝚕$ .
Let $𝒱$ be the set of vertices of $G_{f}$ that were generated from the items of the collection $𝚌𝚘𝚕$ .
- If $𝒱$ is not empty, $𝐏𝐑𝐎𝐃 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$ corresponds to the product of the values of attribute $𝚊𝚝𝚝𝚛$ associated with the vertices of $𝒱$ ,
- Otherwise, if $𝒱$ is empty, $𝐏𝐑𝐎𝐃 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$ is equal to 1.
EXAMPLE: The constraint $𝚙𝚛𝚘𝚍𝚞𝚌𝚝_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$ forces the product of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection to be equal, less than or equal, ... to a given domain variable $𝚅𝙰𝚁$ .

To each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a vertex of the initial graph. Since we want to keep all the vertices of the initial graph we use the $𝑆𝐸𝐿𝐹$ arc generator together with the $𝚃𝚁𝚄𝙴$ arc constraint. Finally, $𝐏𝐑𝐎𝐃 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛) 𝙲𝚃𝚁 𝚅𝙰𝚁$ expresses the required condition. In this expression $𝚟𝚊𝚛$ and $𝙲𝚃𝚁$ respectively corresponds to the attribute of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ (a domain variable) and to the condition we want to enforce. Since the final graph $G_{f}$ contains all the vertices of the initial graph, the expression $𝐏𝐑𝐎𝐃 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)$ corresponds to the product of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection.
$𝐑𝐀𝐍𝐆𝐄 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$
- $𝚌𝚘𝚕$ is a collection that was used for generating the vertices of the initial graph,
- $𝚊𝚝𝚝𝚛$ is an attribute corresponding to an integer or to a domain variable of the collection $𝚌𝚘𝚕$ .
Let $𝒱$ be the set of vertices of $G_{f}$ that were generated from the items of the collection $𝚌𝚘𝚕$ .
- If $𝒱$ is not empty, $𝐑𝐀𝐍𝐆𝐄 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$ corresponds to the difference between the maximum and the minimum values of attribute $𝚊𝚝𝚝𝚛$ associated with the vertices of $𝒱$ ,
- Otherwise, if $𝒱$ is empty, $𝐑𝐀𝐍𝐆𝐄 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$ is equal to 0.
EXAMPLE: The constraint $𝚛𝚊𝚗𝚐𝚎_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$ forces the difference between the maximum value and the minimum value of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection to be equal, less than or equal, ... to a given domain variable $𝚅𝙰𝚁$ .

To each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a vertex of the initial graph. Since we want to keep all the vertices of the initial graph we use the $𝑆𝐸𝐿𝐹$ arc generator together with the $𝚃𝚁𝚄𝙴$ arc constraint. Finally, $𝐑𝐀𝐍𝐆𝐄 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛) 𝙲𝚃𝚁 𝚅𝙰𝚁$ expresses the required condition. In this expression $𝚟𝚊𝚛$ and $𝙲𝚃𝚁$ respectively corresponds to the attribute of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ (a domain variable) and to the condition we want to enforce. Since the final graph $G_{f}$ contains all the vertices of the initial graph, the expression $𝐑𝐀𝐍𝐆𝐄 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)$ corresponds to the difference between the maximum value and the minimum value of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection.
$𝐒𝐔𝐌 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$
- $𝚌𝚘𝚕$ is a collection that was used for generating the vertices of the initial graph,
- $𝚊𝚝𝚝𝚛$ is an attribute corresponding to an integer or to a domain variable of the collection $𝚌𝚘𝚕$ .
Let $𝒱$ be the set of vertices of $G_{f}$ that were generated from the items of the collection $𝚌𝚘𝚕$ .
- If $𝒱$ is not empty, $𝐒𝐔𝐌 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$ corresponds to the sum of the values of attribute $𝚊𝚝𝚝𝚛$ associated with the vertices of $𝒱$ ,
- Otherwise, if $𝒱$ is empty, $𝐒𝐔𝐌 (𝚌𝚘𝚕, 𝚊𝚝𝚝𝚛)$ is equal to 0.
EXAMPLE: The constraint $𝚜𝚞𝚖_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$ forces the sum of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection to be equal, less than or equal, ... to a given domain variable $𝚅𝙰𝚁$ .

To each variable of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a vertex of the initial graph. Since we want to keep all the vertices of the initial graph we use the $𝑆𝐸𝐿𝐹$ arc generator together with the $𝚃𝚁𝚄𝙴$ arc constraint. Finally, $𝐒𝐔𝐌 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛) 𝙲𝚃𝚁 𝚅𝙰𝚁$ expresses the required condition. In this expression $𝚟𝚊𝚛$ and $𝙲𝚃𝚁$ respectively correspond to the attribute of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ (a domain variable) and to the condition we want to enforce. Since the final graph $G_{f}$ contains all the vertices of the initial graph, the expression $𝐒𝐔𝐌 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)$ corresponds to the sum of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection.
$𝐒𝐔𝐌_𝐖𝐄𝐈𝐆𝐇𝐓_𝐀𝐑𝐂 (𝙴𝚡𝚙𝚛)$ $𝙴𝚡𝚙𝚛$ is an arithmetic expression. For each arc $a$ of $E (G_{f})$ , let $f (a)$ denote the value of $𝙴𝚡𝚙𝚛$ . $𝐒𝐔𝐌_𝐖𝐄𝐈𝐆𝐇𝐓_𝐀𝐑𝐂 (𝙴𝚡𝚙𝚛)$ is equal to $\sum_{a \in E (G_{f})} f (a)$ . The value of $𝙴𝚡𝚙𝚛$ usually depends on the attributes of the items located at the extremities of an arc.

EXAMPLE: The constraint $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚠𝚒𝚝𝚑_𝚌𝚘𝚜𝚝𝚜$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂,$ $𝚅𝙰𝙻𝚄𝙴𝚂, 𝙼𝙰𝚃𝚁𝙸𝚇, 𝙲𝙾𝚂𝚃)$ forces that each value $𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚟𝚊𝚕$ be assigned to exactly $𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎$ variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. In addition the $𝙲𝙾𝚂𝚃$ of an assignment is equal to the sum of the elementary costs associated with the fact that we assign the $i^{t h}$ variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection to the $j^{t h}$ value of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection. These elementary costs are given by the $𝙼𝙰𝚃𝚁𝙸𝚇$ collection.

The graph-property $𝚂𝚄𝙼_𝚆𝙴𝙸𝙶𝙷𝚃_𝙰𝚁𝙲 (𝙼𝙰𝚃𝚁𝙸𝚇 [(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚔𝚎𝚢 - 1) * 𝚜𝚒𝚣𝚎 (𝚅𝙰𝙻𝚄𝙴𝚂) + 𝚟𝚊𝚕𝚞𝚎𝚜 . 𝚔𝚎𝚢] . 𝚌) = 𝙲𝙾𝚂𝚃$ expresses that the $𝙲𝙾𝚂𝚃$ variable is equal to the sum of the elementary costs associated with each variable-value assignment. All these elementary costs are recorded in the $𝙼𝙰𝚃𝚁𝙸𝚇$ collection. More precisely, the cost $c_{i j}$ is recorded in the attribute $𝚌$ of the ${((i - 1) * | 𝚅𝙰𝙻𝚄𝙴𝚂) | + j)}^{t h}$ entry of the $𝙼𝙰𝚃𝚁𝙸𝚇$ collection.

A last graph parameter, $𝐃𝐈𝐒𝐓𝐀𝐍𝐂𝐄$ , is computed on two final graphs $G_{1}$ and $G_{2}$ that have the same set $V$ of vertices and the sets $E (G_{1})$ and $E (G_{2})$ of arcs. This graph parameter is the cardinality of the set $(E (G_{1}) - E (G_{2})) \cup (E (G_{2}) - E (G_{1}))$ . This corresponds to the number of arcs that belong to $E (G_{1})$ but not to $E (G_{2})$ , plus the number of arcs that are in $E (G_{2})$ but not in $E (G_{1})$ .

Graph class

For a given global constraint, a graph class specifies a general property that holds on its final digraph. We list the different graph classes and, for each of them, we point to some global constraints that fit in that class. Finding all the global constraints corresponding to a given graph class can be done by looking into the list of keywords (see Section 3.7 on page 3.7).