2.4.1. Selecting an appropriate description
As we previously said, we focus on those global constraints that can be checked by scanning once through their variables. This is for instance the case of:
Since they illustrate key points needed for characterising the set of solutions associated with a global constraint, our discussion will be based on the last five constraints for which we now recall the definition:
The constraint forces the sequence of 0-1 variables to have at most one group of consecutive 1. For instance, the constraint holds since we have only one group of consecutive 1.
The lexicographic ordering constraint (see ) over two vectors of variables and holds if and only if or or and .
The constraint restricts the number of variables of the sequence of variables that take their values in a given set , to be equal to the variable . For instance, holds since exactly 3 values of the sequence 45541 are located in the set of values .
The constraint forces the number of inflexions of the sequence of variables to be equal to the variable . An inflexion is described by one of the following patterns: a strict increase followed by a strict decrease or, conversely, a strict decrease followed by a strict increase. For instance, holds since we can extract from the sequence 33145565563 the four subsequences 314, 565, 6556 and 563, which all follow one of these two patterns.
The constraint forces all pairs of distinct variables of the collection to take distinct values. For instance holds since we have four distinct values.
Figure 2.4.1. Five checkers and their corresponding automata
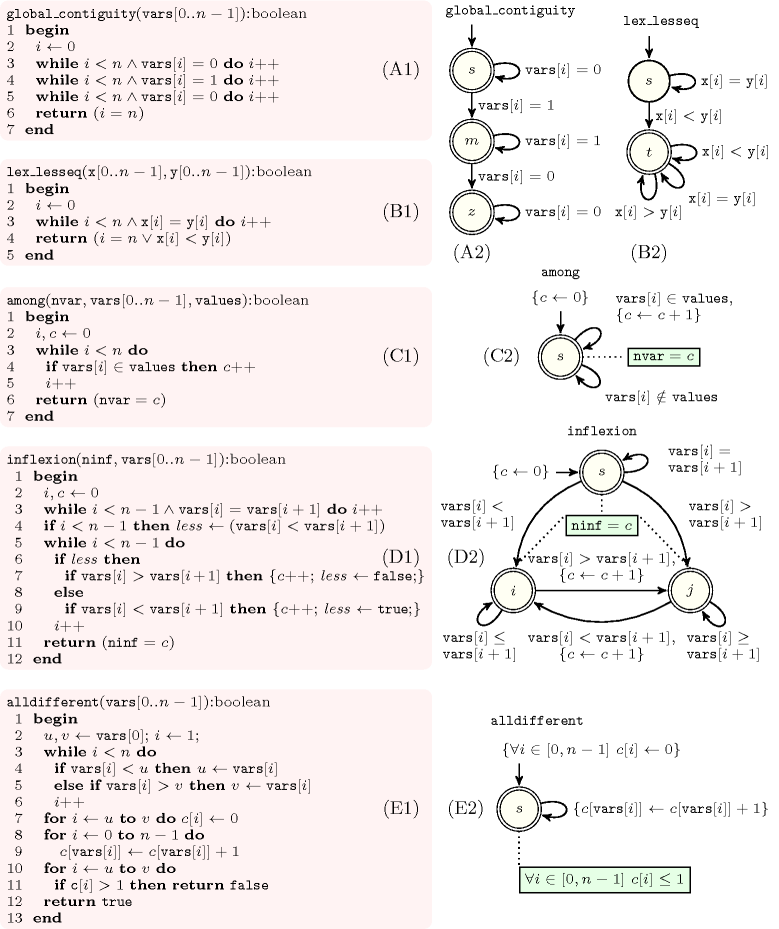
Parts (A1), (B1), (C1), (D1) and (E1) of Figure 2.4.1 depict the five checkers respectively associated with , with , with , with and with . Within the corresponding automata an initial state is indicated by an arc coming from no state and an accepting state is denoted graphically by a double circle. For each checker we observe the following facts:
Within the checker depicted by part (A1) of Figure 2.4.1, the values of the sequence are successively compared against 0 and 1 in order to check that we have at most one group of consecutive 1. This can be translated to the automaton depicted by part (A2) of Figure 2.4.1. The automaton takes as input the sequence , and triggers successively a transition for each term of this sequence. Transitions labelled by 0 and 1 are respectively associated with the conditions and .Transitions leading to failure are systematically skipped. This is why no transition labelled with a 1 starts from state .
Within the checker given by part (B1) of Figure 2.4.1, the components of vectors and are scanned in parallel. We first skip all the components that are equal and then perform a final check. This is represented by the automaton depicted by part (B2) of Figure 2.4.1. The automaton takes as input the sequence and triggers a transition for each term of this sequence. Unlike the constraint, some transitions now correspond to a condition (e.g., , ) between two variables of the constraint.
Note that the constraint involves a variable whose value is computed from a given collection of variables . The checker depicted by part (C1) of Figure 2.4.1 counts the number of variables of that take their values in . For this purpose it uses a counter , which is possibly tested against the value of . This convinced us to allow the use of counters in an automaton. Each counter has an initial value, which can be updated while triggering certain transitions. The accepting states of an automaton can force a variable of the constraint to be equal to a given counter. Part (C2) of Figure 2.4.1 describes the automaton corresponding to the code given in part (C1) of the same figure. The automaton uses the counter variable initially set to 0 and takes as input the sequence . It triggers a transition for each variable of this sequence and increments when the corresponding variable takes its value in . The accepting state returns a success when the value of is equal to . At this point we want to stress the following fact: it would have been possible to use an automaton that avoids the use of counters. However, this automaton would depend on the effective value of the argument . In addition, it would require more states than the automaton of part (C2) of Figure 2.4.1. This is typically a problem if we want to have a fixed number of states in order to save memory as well as time.
As the constraint, the constraint involves a variable whose value is computed from a given sequence of variables . Therefore, the checker depicted in part (D1) of Figure 2.4.1 uses also a counter for counting the number of inflexions, and compares its final value to the argument. The automaton depicted by part (D2) of Figure 2.4.1 represents this program. It takes as input the sequence of pairs and triggers a transition for each pair. Note that a given variable may occur in more than one pair. Each transition compares the respective values of two consecutive variables of and increments the counter when a new inflexion is detected. The accepting state returns a success when the value of is equal to .
The checker associated with is depicted by part (E1) of Figure 2.4.1. It first initialises an array of counters to 0. The entries of the array correspond to the potential values of the sequence . In a second phase the checker computes for each potential value its number of occurrences in the sequence . This is done by scanning this sequence. Finally in a third phase the checker verifies that no value is used more than once. These three phases are represented by the automaton depicted by part (E2) of Figure 2.4.1. The automaton depicted by part (E2) takes as input the sequence . Its initial state initialises an array of counters to 0. Then it triggers successively a transition for each element of the input sequence and increments by 1 the entry corresponding to . The accepting state checks that all entries of the array of counters are strictly less than 2, which means that no value occurs more than once in the sequence .
Synthesising all the observations we got from these examples leads to the following remarks and definitions for a given global constraint :
For a given state, no transition can be triggered indicates that the constraint does not hold.
Since all transitions starting from a given state are mutually incompatible all automata are deterministic. Let denote the set of mutually incompatible conditions associated with the different transitions of an automaton.
Let denote the sequence of subsets of variables of on which the transitions are successively triggered. All these subsets contain the same number of elements and refer to some variables of . Since these subsets typically depend on the constraint, we leave the computation of outside the automaton. To each subset of this sequence corresponds a variable with an initial domain ranging over , where is a fixed integer. To each integer of this range corresponds one of the mutually incompatible conditions of . The sequences and are respectively called the signature and the signature argument of the constraint. The constraint between and the variables of is called the signature constraint and is denoted by .
From a pragmatic point the view, the task of writing a constraint checker is naturally done by writing down an imperative program where local variables, arrays, assignment statements and control structures are used. This suggested us to consider deterministic finite automata augmented with local variables and assignment statements on these variables. Regarding control structures, we did not introduce any extra feature since the deterministic choice of which transition to trigger next seemed to be good enough.
Many global constraints involve a variable whose value is computed from a given collection of variables. This convinced us to allow the accepting state of an automaton to optionally return a result. In practice, this result corresponds to the value of a local variable of the automaton in the accepting state.