Proposition 151

Proof 149 The left-hand side of 151 corresponds to the minimum number of vertices of the two final graphs provided that we build the smallest possible connected components.

Proposition 152

Proof 150 The maximum number of connected components is achieved by building non-empty groups as small as possible, except for two groups of respective size $max(1,\underline{\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_1})$ and $max(1,\underline{\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2})$, which have to be built.

Proposition 153

Proof 151 The left-hand side of 153 corresponds to the maximum number of vertices of the two final graphs provided that we build the largest possible connected components.

Proposition 154

Proof 152 The minimum number of connected components is achieved by taking the groups as large as possible except for two groups of respective size $\overline{\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_2}$ and $\overline{\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_1}$, which have to be built.

Proposition 155

Proof 153 If ${\mathrm{𝐍𝐂𝐂}}_1\le 1$ we have that $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2\le \mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_2$. Otherwise, when ${\mathrm{𝐍𝐂𝐂}}_1>1$, we have that $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_1·max(0,{\mathrm{𝐍𝐂𝐂}}_1-1)+\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_1+\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_2+\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2+\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_2·max(0,{\mathrm{𝐍𝐂𝐂}}_1-3)\le {\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}}_{\mathrm{𝙸𝙽𝙸𝚃𝙸𝙰𝙻}}$. ${\mathrm{𝐍𝐂𝐂}}_1-3$ comes from the fact that we build the minimum number of connected components in the second final graph (i.e., ${\mathrm{𝐍𝐂𝐂}}_1-1$ connected components) and that we have already built two connected components of respective size $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_2$ and $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2$. By isolating $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2$ in the previous expression and by grouping the two inequalities the result follows.

Proposition 156

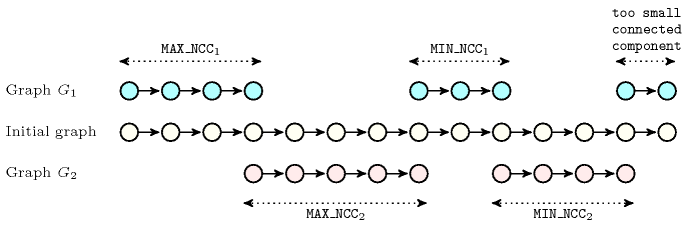
Proof 154 The maximum number of connected components of $G_1$ is achieved by:

• Building a first connected component of $G_1$ involving $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_1$ vertices,

• Building a first connected component of $G_2$ involving $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2$ vertices,

• Building alternatively a connected component of $G_1$ and a connected component of $G_2$ involving respectively $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_1$ and $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_2$ vertices,

• Finally, if this is possible, building a connected component of $G_1$ involving $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_1$ vertices.

Proposition 157

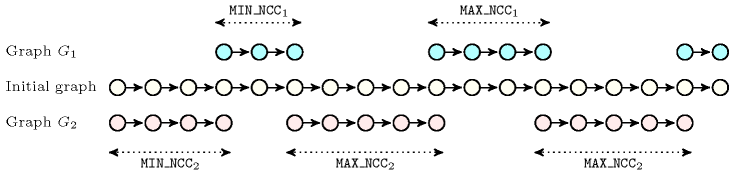
Proof 155 The minimum number of connected components of $G_1$ is achieved by:

• Building a first connected component of $G_2$ involving $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_2$ vertices,

• Building a first connected component of $G_1$ involving $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐂𝐂}}_1$ vertices,

• Building alternatively a connected component of $G_2$ and a connected component of $G_1$ involving respectively $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2$ and $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_1$ vertices,

• Finally, if this is possible, building a connected component of $G_2$ involving $\mathrm{𝐌𝐀𝐗}\_{\mathrm{𝐍𝐂𝐂}}_2$ vertices and a connected component of $G_1$ with the remaining vertices. Note that these remaining vertices cannot be incorporated in the connected components previously built.

Proposition 158

Proof 156 Similar to Proposition 151.

Proposition 159

Proof 157 Similar to Proposition 152.

Proposition 160

Proof 158 Similar to Proposition 153.

Proposition 161

Proof 159 Similar to Proposition 154.

Proposition 162

Proof 160 Similar to Proposition 155.

Proposition 163

Proof 161 Similar to Proposition 156.

Proposition 164

Proof 162 Similar to Proposition 157.