Global Constraint Catalog

2.3.3.2. Dynamic graph constraint

The purpose of a dynamic graph constraint is to enforce a condition on different subsets of variables, not known in advance. This situation occurs frequently in practice and is hard to express since one cannot use a classical constraint for which it is required to provide all variables right from the beginning. One good example of such global constraint is the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint where one wants to force the sum of some variables to be less than or equal to a given limit. In the context of the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint, each set of variables is defined by the height of the different tasks that overlap a given instant $i$ . Since the origins of the tasks are not initially fixed, we do not know in advance which task will overlap a given instant and so, we cannot state any sum constraint initially.

A dynamic graph constraint is defined in exactly the same way as a simple graph constraint, except that we may omit the Graph property(ies) slot, and that we have to provide the two following additional slots:

The Set slot denotes a generator of sets of vertices. Such a generator takes as argument a final graph and produces different sets of vertices. In order to have something tractable, we force the total number of generated sets to be polynomial in the number of vertices.

In practice each set of vertices is represented by a collection of items. The type of this collection corresponds either to the type of the items associated with the vertices, or to the type of a new derived collection. This is achieved by providing an expression of the form $𝚗𝚊𝚖𝚎$ or $𝚗𝚊𝚖𝚎$ - $𝚍𝚎𝚛𝚒𝚟𝚎𝚍_𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗$ , where $𝚗𝚊𝚖𝚎$ represents a formal parameter, and $𝚍𝚎𝚛𝚒𝚟𝚎𝚍_𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗$ a declaration of a new derived collection (as specified in Section 2.3.2.1 on page 2.3.2.1).
The Constraint(s) on sets slot provides a global constraint defined in the catalogue that has to hold for each set created by the previous generator.

We now describe the different generators of sets of vertices currently available:

$𝖠𝖫𝖫_𝖵𝖤𝖱𝖳𝖨𝖢𝖤𝖲$ generates a single set containing all the vertices of the final graph. It is specified by a declaration of the form

$𝖠𝖫𝖫_𝖵𝖤𝖱𝖳𝖨𝖢𝖤𝖲 > > [𝚟𝚎𝚛𝚝𝚒𝚌𝚎𝚜]$

where $𝚟𝚎𝚛𝚝𝚒𝚌𝚎𝚜$ represents all the vertices of the final graph.
$𝖢𝖢$ generates one set of vertices for each connected component of the final graph. These sets correspond to all the vertices of a given connected component. It is specified by a declaration of the form

$𝖢𝖢 > > [𝚌𝚘𝚗𝚗𝚎𝚌𝚝𝚎𝚍_𝚌𝚘𝚖𝚙𝚘𝚗𝚎𝚗𝚝]$

where $𝚌𝚘𝚗𝚗𝚎𝚌𝚝𝚎𝚍_𝚌𝚘𝚖𝚙𝚘𝚗𝚎𝚗𝚝$ represents the vertices of a connected component of the final graph.
$𝖯𝖠𝖳𝖧_𝖫𝖤𝖭𝖦𝖳𝖧 (L)$ generates all elementary pathsA path where all vertices are distinct is called an elementary path. of $L$ vertices of the final graph such that, discarding loops, all vertices of a path (except the last one) have no more than one successor in the final graph. It is specified by a declaration of the form

$𝖯𝖠𝖳𝖧_𝖫𝖤𝖭𝖦𝖳𝖧 (L) > > [𝚙𝚊𝚝𝚑]$

where $𝚙𝚊𝚝𝚑$ represents the vertices of an elementary path, ordered according to their occurrences in the path.
$𝖯𝖱𝖤𝖣$ generates the non-empty sets corresponding to the predecessors of each vertex of the final graph. It is specified by a declaration of the form

$𝖯𝖱𝖤𝖣 > > [𝚙𝚛𝚎𝚍𝚎𝚌𝚎𝚜𝚜𝚘𝚛, 𝚍𝚎𝚜𝚝𝚒𝚗𝚊𝚝𝚒𝚘𝚗]$

where $𝚍𝚎𝚜𝚝𝚒𝚗𝚊𝚝𝚒𝚘𝚗$ represents a vertex of the final graph and $𝚙𝚛𝚎𝚍𝚎𝚌𝚎𝚜𝚜𝚘𝚛$ its predecessors.
$𝖲𝖴𝖢𝖢$ generates the non-empty sets corresponding to the successors of each vertex of the final graph. It is specified by a declaration of the form

$𝖲𝖴𝖢𝖢 > > [𝚜𝚘𝚞𝚛𝚌𝚎, 𝚜𝚞𝚌𝚌𝚎𝚜𝚜𝚘𝚛]$

where $𝚜𝚘𝚞𝚛𝚌𝚎$ represents a vertex of the final graph and $𝚜𝚞𝚌𝚌𝚎𝚜𝚜𝚘𝚛$ its successors.

As an illustrative example of dynamic graph constraint we now consider the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint.

EXAMPLE: The $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ $(𝚃𝙰𝚂𝙺𝚂, 𝙻𝙸𝙼𝙸𝚃)$ constraint, where $𝚃𝙰𝚂𝙺𝚂$ is a collection of the form $𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚍𝚟𝚊𝚛, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 𝚍𝚟𝚊𝚛, 𝚎𝚗𝚍 - 𝚍𝚟𝚊𝚛,$ $𝚑𝚎𝚒𝚐𝚑𝚝 - 𝚍𝚟𝚊𝚛)$ , and where $𝙻𝙸𝙼𝙸𝚃$ is a non-negative integer, holds if, for any point the cumulated height of the set of tasks that overlap that point, does not exceed $𝙻𝙸𝙼𝙸𝚃$ .

The first graph constraint of $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ forces for each task of the $𝚃𝙰𝚂𝙺𝚂$ collection the equality $𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 𝚎𝚗𝚍$ . We focus on the second graph constraint, which uses a dynamic graph constraint described by the following items:

Arc input(s) :

$𝚃𝙰𝚂𝙺𝚂 𝚃𝙰𝚂𝙺𝚂$

Arc generator :

$𝑃𝑅𝑂𝐷𝑈𝐶𝑇 \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜 1, 𝚝𝚊𝚜𝚔𝚜 2)$

Arc arity :

Arc constraint(s) :

$𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 > 0$

$𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗$

$𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 2 . 𝚎𝚗𝚍$

Sets :

$𝖲𝖴𝖢𝖢 > >$

$[𝚜𝚘𝚞𝚛𝚌𝚎,$

$𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 - 𝚌𝚘𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛),$

$[𝚒𝚝𝚎𝚖 (𝚟𝚊𝚛 - 𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝)])]$

Constraint(s) on sets:

$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, \leq, 𝙻𝙸𝙼𝙸𝚃)$

The second graph constraint is defined by:

To each item of the $𝚃𝙰𝚂𝙺𝚂$ collection correspond two vertices of the initial graph.
The arity of the arc constraint is 2.
The arcs of the initial graph are constructed with the $𝑃𝑅𝑂𝐷𝑈𝐶𝑇$ arc generator between the $𝚃𝙰𝚂𝙺𝚂$ collection and the $𝚃𝙰𝚂𝙺𝚂$ collection. Therefore, each vertex associated with a task is linked to all the vertices related to the different tasks.
The arc constraint that is associated with an arc between a task $𝚝𝚊𝚜𝚔𝚜 1$ and a task $𝚝𝚊𝚜𝚔𝚜 2$ is an overlapping constraint that holds if both, the duration of $𝚝𝚊𝚜𝚔𝚜 1$ is strictly greater than zero, and if the origin of $𝚝𝚊𝚜𝚔𝚜 1$ is overlapped by task $𝚝𝚊𝚜𝚔𝚜 2$ .
The set generator is $𝖲𝖴𝖢𝖢$ . The final graph will consist of those tasks for which the origin is covered by at least one task and of those corresponding tasks.
The dynamic constraint on a set forces the sum of the heights of the tasks that belong to a successor set to not exceed $𝙻𝙸𝙼𝙸𝚃$ .

Figure 2.3.6. Initial and final graph of an instance of the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint

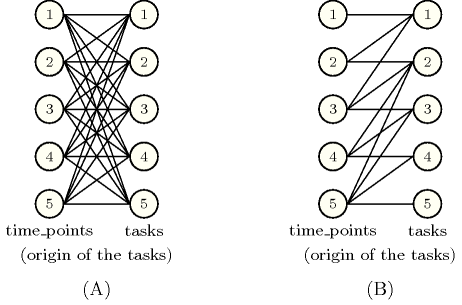
Parts (A) and (B) of Figure 2.3.6 respectively show the initial and the final graph corresponding to the following instance:

$𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ $(〈 𝚘𝚛𝚒𝚐𝚒𝚗 - 1 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 3 𝚑𝚎𝚒𝚐𝚑𝚝 - 1,$

$𝚘𝚛𝚒𝚐𝚒𝚗 - 2 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 9 𝚑𝚎𝚒𝚐𝚑𝚝 - 2,$

$𝚘𝚛𝚒𝚐𝚒𝚗 - 3 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 10 𝚑𝚎𝚒𝚐𝚑𝚝 - 1,$

$𝚘𝚛𝚒𝚐𝚒𝚗 - 6 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 6 𝚑𝚎𝚒𝚐𝚑𝚝 - 1,$

$𝚘𝚛𝚒𝚐𝚒𝚗 - 7 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2 𝚑𝚎𝚒𝚐𝚑𝚝 - 3 〉, 8) .$

We label the vertices of the initial and final graph by giving the $𝚔𝚎𝚢$ $𝚔𝚎𝚢$ is an implicit attribute corresponding to the position of an item within a collection that was introduced in Section 2.2.2 on page 2.2.2. of the corresponding task. On both graphs the edges are oriented from left to right. On the final graph we consider the sets that consist of the successors of the different vertices; those are the sets of tasks ${1}$ , ${1, 2}$ , ${1, 2, 3}$ , ${2, 3, 4}$ and ${2, 3, 4, 5}$ . Since the $𝖲𝖴𝖢𝖢$ set generator uses a derived collection that only considers the $𝚑𝚎𝚒𝚐𝚑𝚝$ attribute of a task, these sets respectively correspond to the following collection of items:

$〈 𝚟𝚊𝚛 - 1 〉$ ,
$〈 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 2 〉$ ,
$〈 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 2, 𝚟𝚊𝚛 - 1 〉$ ,
$〈 𝚟𝚊𝚛 - 2, 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 1 〉$ ,
$〈 𝚟𝚊𝚛 - 2, 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 3 〉$ .

The $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint holds since, for each successors set, the corresponding constraint holds:

$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(〈 𝚟𝚊𝚛 - 1 〉, \leq, 8)$ ,
$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(〈 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 2 〉, \leq, 8)$ ,
$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(〈 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 2, 𝚟𝚊𝚛 - 1 〉, \leq, 8)$ ,
$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(〈 𝚟𝚊𝚛 - 2, 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 1 〉, \leq, 8)$ ,
$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(〈 𝚟𝚊𝚛 - 2, 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 1, 𝚟𝚊𝚛 - 3 〉, \leq, 8)$ .

The $𝚜𝚞𝚖_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$ constraint holds if the sum $𝚂$ of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection satisfies $𝚂 𝙲𝚃𝚁 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ , where $𝙲𝚃𝚁$ is a comparison operator.

Global Constraint Catalog

2. Describing Global Constraints

2.3.3.2. Dynamic graph constraint

Figure 2.3.6. Initial and final graph of an instance of the 𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎 constraint

Figure 2.3.6. Initial and final graph of an instance of the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint