2.3.2.3. Graph generators

This section describes how to generate the initial graph associated with a global constraint. Initial graphs correspond to directed hypergraphs [Berge87], which have a very regular structure. They are defined in the following way:

• The vertices of the directed hypergraph are generated from collections of items such that each item corresponds to one vertex of the directed hypergraph. These collections are either collections that arise as arguments of the global constraint, or collections that are derived from one or several arguments of the global constraint. In this latter case these derived collections are computed by using the collection generators previously introduced (see Section 2.3.2.1 on page 2.3.2.1).

• To all arcs of the directed hypergraph corresponds the same arc constraint that involves vertices in a given order.Usually the edges of a hypergraph are not oriented [Berge87]. However for our purpose we need to define an order on the vertices of an edge since the corresponding arc constraint takes its arguments in a given order. These arc constraints, which are mainly unary and binary constraints, were described in the previous section (see Section 2.3.2.2 on page 2.3.2.2). We describe all the arcs of an initial graph with a set of predefined arc generators, which correspond to classical regular structures one can find in the graph literature [Skiena90]. An arc generator of arity $a$ takes $n$ collections of items, denoted ${𝚌}_i(1\le i\le n)$, as input and returns the corresponding hypergraph where the vertices are the items of the input collections ${𝚌}_i(1\le i\le n)$ and where all arcs involve $a$ vertices. Specific arc generators allow for giving an $a$-ary constraint for which $a$ is not fixed, which means that the corresponding hypergraph contains arcs involving various number of vertices.

Each arc generator has a name and takes one or several collections of items as input and generates a set of arcs. Each arc is made from a sequence of items $i_1{i}_2\cdots i_a$ and is denoted by $(i_1,i_2,\cdots ,i_a)$. $a$ is called the arity of the arc generator. We have the following types of arc generators:

• Arc generators with a fixed predefined arity. In fact most arc generators have a fixed predefined arity of 2. The graphs they generate correspond to digraphs.

• Arc generators that can be used with any arity $a$ greater than or equal to 1. These arc generators generate directed hypergraphs where all arcs consist of $a$ items.

• Arc generators that generate arcs that do not involve the same number of items.

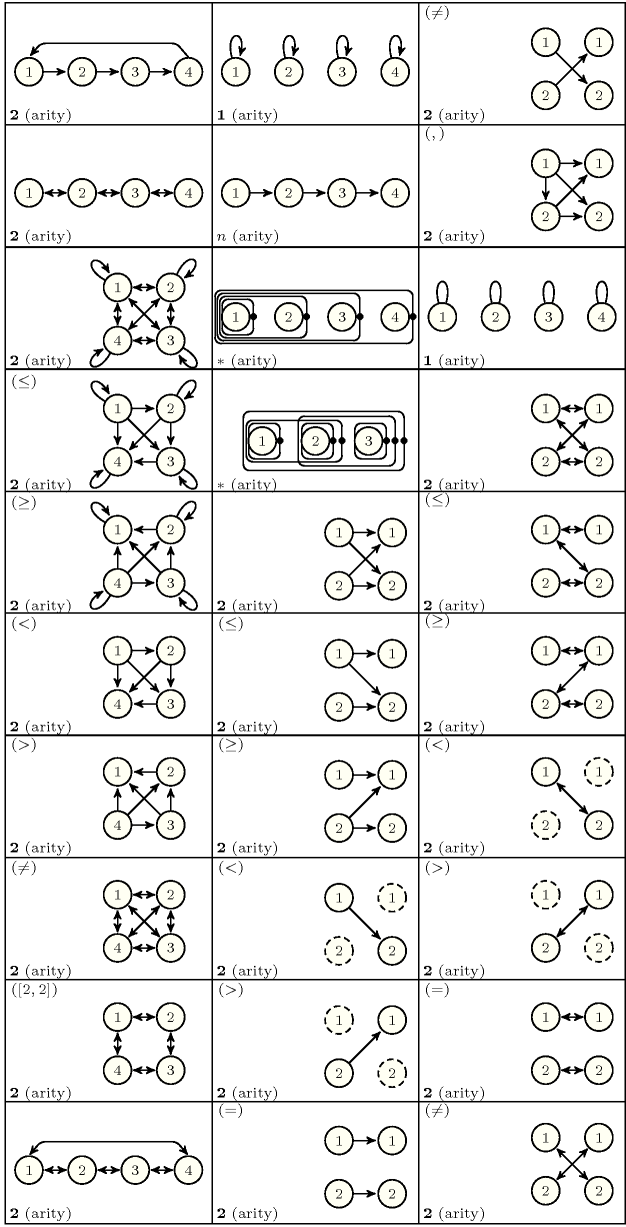
We now give the list of arc generators, listed in alphabetic order, and the arcs they generate. For each arc generator we point to a global constraint where it is used in practice. Finally, Figure 2.3.4 illustrates the different arc generators. At present the following arc generators are in use:

• $\mathrm{𝐶𝐻𝐴𝐼𝑁}$ has a predefined arity of 2. It takes one collection $𝚌$ and generates the following arcsAs defined in Section 2.2.2 on page 2.2.2 we use the following notation: for a given collection $𝚌$, $\left|𝚌\right|$ and $𝚌\left[i\right]$ respectively denote the number of items of $𝚌$ and the $i^{th}$ item of $𝚌$.:

  • $\forall i\in [1,|𝚌|-1]$: $\left(𝚌\right[i],𝚌[i+1\left]\right)$,

  • $\forall i\in [1,|𝚌|-1]$: $\left(𝚌\right[i+1],𝚌[i\left]\right)$.

  EXAMPLE: The arc generator $\mathrm{𝐶𝐻𝐴𝐼𝑁}$ is for instance used in the $\mathrm{𝚐𝚛𝚘𝚞𝚙}\_\mathrm{𝚜𝚔𝚒𝚙}\_\mathrm{𝚒𝚜𝚘𝚕𝚊𝚝𝚎𝚍}\_\mathrm{𝚒𝚝𝚎𝚖}$ constraint.

• $\mathrm{𝐶𝐼𝑅𝐶𝑈𝐼𝑇}$ has a predefined arity of 2. It takes one collection $𝚌$ and generates the following arcs:

  • $\forall i\in [1,|𝚌|-1]$: $\left(𝚌\right[i],𝚌[i+1\left]\right)$,

  • $\left(𝚌\right[\left|𝚌\right|],𝚌[1\left]\right)$.

  EXAMPLE: The arc generator $\mathrm{𝐶𝐼𝑅𝐶𝑈𝐼𝑇}$ is for instance used in the $\mathrm{𝚌𝚒𝚛𝚌𝚞𝚕𝚊𝚛}\_\mathrm{𝚌𝚑𝚊𝚗𝚐𝚎}$ constraint.

• $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}$ can be used with any arity $a$ greater than or equal to 2. It takes one collection $𝚌$ and generates the arcs: $\forall i_1\in [1,|𝚌\left|\right],\forall i_2\in [1,|𝚌\left|\right],\cdots ,\forall i_a\in [1,|𝚌\left|\right]:(𝚌\left[i_1\right],𝚌\left[i_2\right],\cdots ,𝚌\left[i_a\right])$.

  EXAMPLE: The arc generator $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}$ is usually used with an arity $a=2$. This is for instance the case of the $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint.

• $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}\left(\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}\right)$, where $\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}$ is one of the comparison operators $\le$, $\ge$, $<$, $>$, $=$, $\ne$, can be used with any arity $a$ greater than or equal to 2. It takes one collection $𝚌$ and generates the arcs:

  $\forall i_1\in [1,|𝚌\left|\right],$

  $\forall i_2\in [1,|𝚌\left|\right]$ such that $i_1\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}{i}_2,$

  $\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots ,$

  $\forall i_a\in [1,|𝚌\left|\right]$ such that $i_{a-1}\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}{i}_a:(𝚌\left[i_1\right],𝚌\left[i_2\right],\cdots ,𝚌\left[i_a\right])$.

  EXAMPLE: The $\mathrm{𝚘𝚛𝚌𝚑𝚊𝚛𝚍}$$\left(\mathrm{𝚃𝚁𝙴𝙴𝚂}\right)$ constraint is an example of constraint that uses the $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}(<)$ arc generator with an arity $a=3$. It generates an arc for each set of three trees.

• $\mathrm{𝐶𝑌𝐶𝐿𝐸}$ has a predefined arity of 2. It takes one collection $𝚌$ and generates the following arcs:

  • $\forall i\in [1,|𝚌|-1]$ $\left(𝚌\right[i],𝚌[i+1\left]\right)$ and $\left(𝚌\right[i+1],𝚌[i\left]\right)$,

  • $\left(𝚌\right[\left|𝚌\right|],𝚌[1\left]\right)$ and $\left(𝚌\right[1],𝚌[\left|𝚌\right|\left]\right)$.

  The arc generator $\mathrm{𝐶𝑌𝐶𝐿𝐸}$ is currently not used.

• $\mathrm{𝐺𝑅𝐼𝐷}\left([d_1,d_2,\cdots ,d_n]\right)$ takes a collection $𝚌$ consisting of $d_1·d_2·\cdots ·d_n$ items and generates the arcs $\left(𝚌\right[i],𝚌[j\left]\right)$ where $i$ and $j$ satisfy the following condition. There exists an integer $\alpha$ $(0\le \alpha \le n-1)$ such that (1) and (2) hold:

  $\left(1\right)|i-j|={\prod }_{1\le k\le \alpha }{d}_k$ (when $\alpha =0$ we have ${\prod }_{1\le k\le \alpha }=1$),

  $\left(2\right)\lfloor \frac{i}{{\prod }_{1\le k\le \alpha +1}{d}_k}\rfloor =\lfloor \frac{j}{{\prod }_{1\le k\le \alpha +1}{d}_k}\rfloor$.

  EXAMPLE: The $\mathrm{𝚌𝚘𝚗𝚗𝚎𝚌𝚝}\_\mathrm{𝚙𝚘𝚒𝚗𝚝𝚜}$ constraint uses the $\mathrm{𝐺𝑅𝐼𝐷}$ arc generator.

• $\mathrm{𝐿𝑂𝑂𝑃}$ has a predefined arity of 2. It takes one collection $𝚌$ and generates the arcs: $\forall i\in [1,|𝚌\left|\right]$: $\left(𝚌\right[i],𝚌[i\left]\right)$. $\mathrm{𝐿𝑂𝑂𝑃}$ is usually used in order to generate a loop on some vertices, so that they do not disappear from the final graph.

  EXAMPLE: The $\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚘𝚗𝚝𝚒𝚐𝚞𝚒𝚝𝚢}$$\left(\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}\right)$ constraint is an example of constraint that uses the $\mathrm{𝐿𝑂𝑂𝑃}$ arc generator so that each variable of the $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}$ collection belongs to the final graph.

• $\mathrm{𝑃𝐴𝑇𝐻}$ can be used with any arity $a$ greater than or equal to 1. It takes one collection $𝚌$, and generates the following arcs: $\forall i\in [1,|𝚌|-a+1]:\left(𝚌\right[i],𝚌[i+1],\cdots ,𝚌[i+a-1\left]\right)$.

  EXAMPLE: $\mathrm{𝑃𝐴𝑇𝐻}$ is for instance used in the $\mathrm{𝚜𝚕𝚒𝚍𝚒𝚗𝚐}\_\mathrm{𝚜𝚞𝚖}$$(\mathrm{𝙻𝙾𝚆},$ $\mathrm{𝚄𝙿},$ $\mathrm{𝚂𝙴𝚀},$ $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂})$ constraint with an arity $\mathrm{𝚂𝙴𝚀}$, where $\mathrm{𝚂𝙴𝚀}$ is an argument of the $\mathrm{𝚜𝚕𝚒𝚍𝚒𝚗𝚐}\_\mathrm{𝚜𝚞𝚖}$ constraint.

• $\mathrm{𝑃𝐴𝑇𝐻}\_\mathit{1}$ generates arcs that do not involve the same number of items. It takes one collection $𝚌$, and generates the following arcs: $\left(𝚌\right[1\left]\right),\left(𝚌\right[1],𝚌[2\left]\right),\cdots ,$ $\left(𝚌\right[1],$ $𝚌\left[2\right],$ $\cdots ,$ $𝚌\left[\right|𝚌\left|\right])$.

  EXAMPLE: $\mathrm{𝑃𝐴𝑇𝐻}\_\mathit{1}$ is used in the

  $\mathrm{𝚜𝚒𝚣𝚎}\_\mathrm{𝚖𝚊𝚡}\_\mathrm{𝚜𝚝𝚊𝚛𝚝𝚒𝚗𝚐}\_\mathrm{𝚜𝚎𝚚}\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint.

• $\mathrm{𝑃𝐴𝑇𝐻}\_𝑁$ generates arcs that do not involve the same number of items. It takes one collection $𝚌$, and generates the following arcs: $\forall i\in [1,|𝚌\left|\right],\forall j\in [i,|𝚌\left|\right]:$ $\left(𝚌\right[i],$ $𝚌[i+1],$ $\cdots ,$ $𝚌\left[j\right])$.

  EXAMPLE: $\mathrm{𝑃𝐴𝑇𝐻}\_𝑁$ is for instance used in the $\mathrm{𝚜𝚒𝚣𝚎}\_\mathrm{𝚖𝚊𝚡}\_\mathrm{𝚜𝚎𝚚}\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint.

• $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$ has a predefined arity of 2. It takes two collections ${𝚌}_1$, ${𝚌}_2$ and generates the arcs: $\forall i\in [1,|{𝚌}_1\left|\right],\forall j\in [1,|{𝚌}_2\left|\right]:({𝚌}_1\left[i\right],{𝚌}_2\left[j\right])$.

  EXAMPLE: $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$ is for instance used in the $\mathrm{𝚜𝚊𝚖𝚎}$$(\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}\mathtt{1},$ $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}\mathtt{2})$ constraint for generating an arc from every item of the $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}\mathtt{1}$ collection to every item of the $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}\mathtt{2}$ collection.

• $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}\left(\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}\right)$, where $\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}$ is one of the comparison operators $\le$, $\ge$, $<$, $>$, $=$, $\ne$, has a predefined arity of 2. It takes two collections ${𝚌}_1$, ${𝚌}_2$ and generates the arcs: $\forall i\in [1,|{𝚌}_1\left|\right],\forall j\in [1,|{𝚌}_2\left|\right]$ such that $i\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}j:({𝚌}_1\left[i\right],{𝚌}_2\left[j\right])$.

  EXAMPLE: $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$$(=)$ is for instance used in the $\mathrm{𝚍𝚒𝚏𝚏𝚎𝚛}\_\mathrm{𝚏𝚛𝚘𝚖}\_\mathrm{𝚊𝚝}\_\mathrm{𝚕𝚎𝚊𝚜𝚝}\_𝚔\_\mathrm{𝚙𝚘𝚜}$$(𝙺,\mathrm{𝚅𝙴𝙲𝚃𝙾𝚁}\mathtt{1},\mathrm{𝚅𝙴𝙲𝚃𝙾𝚁}\mathtt{2})$ constraint in order to generate an arc between the $i^{th}$ component of $\mathrm{𝚅𝙴𝙲𝚃𝙾𝚁}\mathtt{1}$ and the $i^{th}$ component of $\mathrm{𝚅𝙴𝙲𝚃𝙾𝚁}\mathtt{2}$.

• $\mathrm{𝑆𝐸𝐿𝐹}$ has a predefined arity of 1. It takes one collection $𝚌$ and generates the arcs: $\forall i\in [1,|𝚌\left|\right]$: $\left(𝚌\right[i\left]\right)$.

  EXAMPLE: $\mathrm{𝑆𝐸𝐿𝐹}$ is for instance used in the $\mathrm{𝚊𝚖𝚘𝚗𝚐}$$(\mathrm{𝙽𝚅𝙰𝚁},\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂},\mathrm{𝚅𝙰𝙻𝚄𝙴𝚂})$ constraint in order to generate a unary arc constraint $\mathrm{𝚒𝚗}$$(\mathrm{𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜}.\mathrm{𝚟𝚊𝚛},\mathrm{𝚅𝙰𝙻𝚄𝙴𝚂})$ for each variable of the $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}$ collection.

• $\mathrm{𝑆𝑌𝑀𝑀𝐸𝑇𝑅𝐼𝐶}\_\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$ has a predefined arity of 2. It takes two collections ${𝚌}_1$, ${𝚌}_2$ and generates the following arcs: $\forall i\in [1,|{𝚌}_1\left|\right],\forall j\in [1,|{𝚌}_2\left|\right]:({𝚌}_1\left[i\right],{𝚌}_2\left[j\right])$ and $({𝚌}_2\left[j\right],{𝚌}_1\left[i\right])$.

  EXAMPLE: $\mathrm{𝑆𝑌𝑀𝑀𝐸𝑇𝑅𝐼𝐶}\_\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$ is for instance used in the $\mathrm{𝚒𝚗𝚟𝚎𝚛𝚜𝚎}\_\mathrm{𝚠𝚒𝚝𝚑𝚒𝚗}\_\mathrm{𝚛𝚊𝚗𝚐𝚎}$ constraint.

• $\mathrm{𝑆𝑌𝑀𝑀𝐸𝑇𝑅𝐼𝐶}\_\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}\left(\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}\right)$, where $\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}$ is one of the comparison operators $\le$, $\ge$, $<$, $>$, $=$, $\ne$, has a predefined arity of 2. It takes two collections ${𝚌}_1$, ${𝚌}_2$ and generates the arcs: $\forall i\in [1,|{𝚌}_1\left|\right],\forall j\in [1,|{𝚌}_2\left|\right]$ such that $i\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}j:({𝚌}_1\left[i\right],{𝚌}_2\left[j\right])$ and $({𝚌}_2\left[j\right],{𝚌}_1\left[i\right])$.

  EXAMPLE: The $\mathrm{𝚝𝚠𝚘}\_\mathrm{𝚘𝚛𝚝𝚑}\_\mathrm{𝚍𝚘}\_\mathrm{𝚗𝚘𝚝}\_\mathrm{𝚘𝚟𝚎𝚛𝚕𝚊𝚙}$ constraint is an example of constraint that uses the $\mathrm{𝑆𝑌𝑀𝑀𝐸𝑇𝑅𝐼𝐶}\_\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$$(=)$ arc generator.

• $\mathrm{𝑉𝑂𝐼𝐷}$ takes one collection and does not generate any arc.

  EXAMPLE: $\mathrm{𝑉𝑂𝐼𝐷}$ is for instance used in the $\mathrm{𝚕𝚎𝚡}\_\mathrm{𝚕𝚎𝚜𝚜𝚎𝚚}$ constraint.

Finally, we can combine the $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$ arc generator with the arc generators from the following set $𝒢\mathrm{𝑒𝑛𝑒𝑟𝑎𝑡𝑜𝑟}=$ $\{\mathrm{𝐶𝐼𝑅𝐶𝑈𝐼𝑇}$, $\mathrm{𝐶𝐻𝐴𝐼𝑁}$, $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}$, $\mathrm{𝐿𝑂𝑂𝑃}$, $\mathrm{𝑃𝐴𝑇𝐻}$, $\mathrm{𝑉𝑂𝐼𝐷}$$\}$. This is achieved by using the construction $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}({𝙶}_1,{𝙶}_2)$ where ${𝙶}_1$ and ${𝙶}_2$ belong to $𝒢\mathrm{𝑒𝑛𝑒𝑟𝑎𝑡𝑜𝑟}$. It applies ${𝙶}_1$ to the first collection ${𝚌}_1$ passed to $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$ and ${𝙶}_2$ to the second collection ${𝚌}_2$ passed to $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$. Finally, it applies $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$ on ${𝚌}_1$ and ${𝚌}_2$. In a similar way the $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$$\left(\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗}\right)$ arc generator is extended to $\mathrm{𝑃𝑅𝑂𝐷𝑈𝐶𝑇}$$({𝙶}_1,$ ${𝙶}_2,$ $\mathrm{𝙲𝚘𝚖𝚙𝚊𝚛𝚒𝚜𝚘𝚗})$.

Figure 2.3.3. Example of initial graph generated by $\mathrm{𝙿𝚁𝙾𝙳𝚄𝙲𝚃}(\mathrm{𝙲𝙻𝙸𝚀𝚄𝙴},\mathrm{𝙻𝙾𝙾𝙿},=)$ when applied to collections $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}\mathtt{1}$ and $\mathrm{𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂}\mathtt{2}$

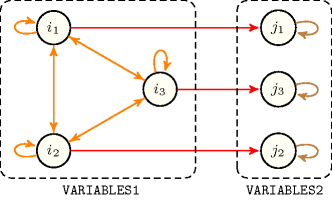
Figure 2.3.4 illustrates the different arc generators. On the one hand, for those arc generators that take a single collection, we apply them on the collection of items $\langle i-1,i-2,i-3,i-4\rangle$. On the other hand, for those arc generators that take two collections, we apply them on $\langle i-1,i-2\rangle$ and $\langle i-3,i-4\rangle$. We use the following pictogram for the graphical representation of a constraint network:

• A line for an arc constraint of arity 1,

• An arrow for an arc constraint of arity 2,

• A closed line for an arc constraint with an arity strictly greater than 2. In this last case, since the vertices of an arc are ordered, a black circle at one of the extremities indicates the direction of the closed line. For instance consider the example of $\mathrm{𝑃𝐴𝑇𝐻}\_\mathit{1}$ in Figure 2.3.4. The closed line that contains vertices 1, 2 and 3 means that a 3-ary arc constraint involves items 1, 2, and 3 in this specific order.

Dotted circles represent vertices that do not belong to the graph. This stems from the fact that the arc generator did not produce any arc involving these vertices. The leftmost lowest corner indicates the arity of the corresponding arc generator:

• An integer if it has a fixed predefined arity,

• $n$ if it can be used with any arity greater than or equal to 1,

• $*$ if it generates arcs that do not necessarily involve the same number of items.

Figure 2.3.4. Examples of arc generators