Global Constraint Catalog

4.4.1. Functional dependency invariants involving two constraints

Proposition 167 Given the constraints

$𝚒𝚗𝚏𝚕𝚎𝚡𝚒𝚘𝚗$ $(𝙽𝙸𝙽𝙵, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙽𝚅𝙰𝙻 = 1 \Rightarrow 𝙽𝙸𝙽𝙵 = 0

Proof 165 Since a single value leads to a plateau.

Proposition 168 Given the constraints

$𝚕𝚎𝚗𝚐𝚝𝚑_𝚏𝚒𝚛𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

2 \cdot 𝙿 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝙻𝙴𝙽

Proof 166 Beside a first sequence with a small value, we alternate between large and small values in order to maximise the number of peaks.

Proposition 169 Given the constraints

$𝚕𝚎𝚗𝚐𝚝𝚑_𝚏𝚒𝚛𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

2 \cdot 𝚅 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝙻𝙴𝙽

Proof 167 Beside a first sequence with a large value, we alternate between small and large values in order to maximise the number of valleys.

Proposition 170 Given the constraints

$𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

2 \cdot 𝙿 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝙻𝙴𝙽

Proof 168 Beside a last sequence with a small value, we alternate between large and small values in order to maximise the number of peaks.

Proposition 171 Given the constraints

$𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

2 \cdot 𝚅 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 𝙻𝙴𝙽

Proof 169 Beside a last sequence with a large value, we alternate between small and large values in order to maximise the number of valleys.

Proposition 172 Given the constraints

$𝚕𝚘𝚗𝚐𝚎𝚜𝚝_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚖𝚊𝚡_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ $(𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙻 \geq 𝙼𝙰𝚇

Proof 170 By definition of the $𝚕𝚘𝚗𝚐𝚎𝚜𝚝_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ and $𝚖𝚊𝚡_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ constraints.

Proposition 173 Given the constraints

$𝚕𝚘𝚗𝚐𝚎𝚜𝚝_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ $(𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙻 \geq 𝙼𝙰𝚇

Proof 171 By definition of the $𝚕𝚘𝚗𝚐𝚎𝚜𝚝_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ and $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ constraints.

Proposition 174 Given the constraints

$𝚖𝚊𝚡_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ $(𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚖𝚒𝚗_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙼𝙰𝚇 \geq 𝙼𝙸𝙽

Proof 172 By definition of the $𝚖𝚊𝚡_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ and $𝚖𝚒𝚗_𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ constraints.

Proposition 175 Given the constraints

$𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ $(𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚖𝚒𝚗_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙼𝙰𝚇 \geq 𝙼𝙸𝙽

Proof 173 By definition of the $𝚖𝚊𝚡_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ and $𝚖𝚒𝚗_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚕𝚘𝚙𝚎$ constraints.

Proposition 176 Given the constraints

$𝚖𝚊𝚡𝚒𝚖𝚞𝚖$ $(𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙼𝙰𝚇 \geq 𝙼𝙸𝙽

Proof 174 By definition of the $𝚖𝚊𝚡𝚒𝚖𝚞𝚖$ and the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraints.

Proposition 177 Given the constraints

$𝚖𝚊𝚡𝚒𝚖𝚞𝚖$ $(𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, =, 𝚂𝚄𝙼)$ :

𝚂𝚄𝙼 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \cdot 𝙼𝙰𝚇

Proof 175 By definition of the $𝚖𝚊𝚡𝚒𝚖𝚞𝚖$ and $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraints.

Proposition 178 Given the constraints

$𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚜𝚞𝚖_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, =, 𝚂𝚄𝙼)$ :

𝚂𝚄𝙼 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \cdot 𝙼𝙸𝙽

Proof 176 By definition of the $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ and $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraints.

Proposition 179 Given the constraints

$𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ $(𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙿 \cdot 𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

Proof 177 Cumulated minimum width of the different peaks cannot exceed size of sequence.

Proposition 180 Given the constraints

$𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ $(𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

The automaton depicted by Figure 4.4.1 provides a necessary condition.

Figure 4.4.1. Automaton for a redundant constraint between the $𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ and the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ $(𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ constraints when $\underset{̲}{𝙿} > 0$ and $\underset{̲}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} > 0$ , where $𝑐𝑜𝑛𝑑$ is the condition $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - i > max (0, max (\underset{̲}{𝙿} - max (S - 1, 0), 0) - 1) \cdot (\underset{̲}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} + 1) + (max (\underset{̲}{𝙿} - max (S - 1, 0), 0) \geq 1) \cdot (\underset{̲}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} - max (i - F, 0))$ , and where $i$ , $S$ and $F$ respectively stand for the index of the current pairs ( $i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1]$ ), the number of start of potential peaks already encountered, the position of the start of the last potential peak encountered; the quantity $max (S - 1, 0)$ denotes the number of peaks already encountered, while the quantity $max (\underset{̲}{𝙿} - max (S - 1, 0), 0)$ denotes the minimum number of peaks that remain to done from position $i$ .

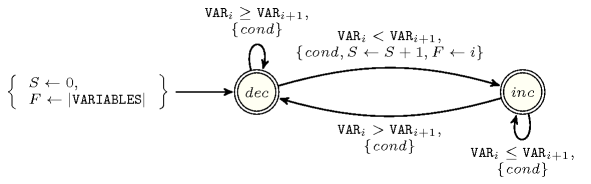
Proof 178 The condition associated with each transition of the automaton checks that there is enough space between the current position and the end of the sequence to place the remaining minimum number of required peaks.

Proposition 181 Given the constraints

$𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝚅 \cdot 𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

Proof 179 Cumulated minimum width of the different valleys cannot exceed size of sequence.

Proposition 182 Given the constraints

$𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

The automaton depicted by Figure 4.4.2 provides a necessary condition.

Figure 4.4.2. Automaton for a redundant constraint between the $𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ and the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ constraints when $\underset{̲}{𝚅} > 0$ and $\underset{̲}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} > 0$ , where $𝑐𝑜𝑛𝑑$ is the condition $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - i > max (0, max (\underset{̲}{𝚅} - max (S - 1, 0), 0) - 1) \cdot \underset{̲}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} + (max (\underset{̲}{𝚅} - max (S - 1, 0), 0) \geq 1) \cdot (\underset{̲}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} - max (i - F, 0))$ , and where $i$ , $S$ and $F$ respectively stand for the index of the current pairs ( $i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1]$ ), the number of start of potential valleys already encountered, the position of the start of the last potential valley encountered; the quantity $max (S - 1, 0)$ denotes the number of valleys already encountered, while the quantity $max (\underset{̲}{𝚅} - max (S - 1, 0), 0)$ denotes the minimum number of valleys that remain to done from position $i$ .

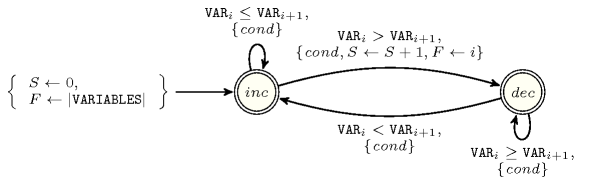
Proof 180 The condition associated with each transition of the automaton checks that there is enough space between the current position and the end of the sequence to place the remaining minimum number of required valleys.

Proposition 183 Given the constraints

$𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚗𝚟𝚒𝚜𝚒𝚋𝚕𝚎_𝚏𝚛𝚘𝚖_𝚎𝚗𝚍$ $(𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙽𝚅𝙰𝙻 \geq 𝙽

Proof 181 Since stairs visible from the end are located at different altitudes.

Proposition 184 Given the constraints

$𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚗𝚟𝚒𝚜𝚒𝚋𝚕𝚎_𝚏𝚛𝚘𝚖_𝚜𝚝𝚊𝚛𝚝$ $(𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

𝙽𝚅𝙰𝙻 \geq 𝙽

Proof 182 Since stairs visible from the start are located at different altitudes.

Proposition 185 Given the constraints

$𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ :

| 𝙿 - 𝚅 | \leq 1

Proof 183 Since peaks and valleys can only alternate.

Proposition 186 Given the constraints

$𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,

with $𝙿 > 𝚅$ , the automaton depicted by Figure 4.4.3 provides a necessary condition.

Figure 4.4.3. Automaton for a redundant constraint for the conjunction $𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) \land$ $𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) \land 𝙿 > 𝚅$ (we have both to start with a peak and to finish with a peak)

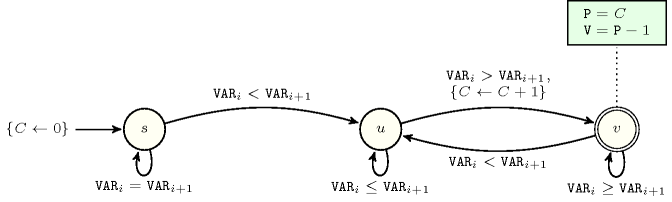
Proof 184 Since peaks and valleys can only alternate and since having more peaks than valleys enforces to start and end on a peak.

Proposition 187 Given the constraints

$𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,
$𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ ,

with $𝚅 > 𝙿$ the automaton depicted by Figure 4.4.4 provides a necessary condition.

Figure 4.4.4. Automaton for a redundant constraint for the conjunction $𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) \land$ $𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) \land 𝚅 > 𝙿$ (we have both to start with a valley and to finish with a valley)

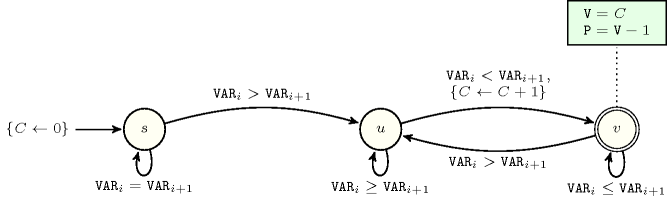
Proof 185 Since valleys and peaks can only alternate and since having more valleys than peaks enforces to start and end on a valley.

Global Constraint Catalog

4. Further Topics

4.4.1. Functional dependency invariants involving two constraints

Figure 4.4.3. Automaton for a redundant constraint for the conjunction 𝚙𝚎𝚊𝚔(𝙿,𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) ∧ 𝚟𝚊𝚕𝚕𝚎𝚢(𝚅,𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) ∧ 𝙿>𝚅 (we have both to start with a peak and to finish with a peak)

Figure 4.4.4. Automaton for a redundant constraint for the conjunction 𝚟𝚊𝚕𝚕𝚎𝚢(𝚅,𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) ∧ 𝚙𝚎𝚊𝚔(𝙿,𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) ∧ 𝚅>𝙿 (we have both to start with a valley and to finish with a valley)

Figure 4.4.3. Automaton for a redundant constraint for the conjunction $𝚙𝚎𝚊𝚔$ $(𝙿, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) \land$ $𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂) \land 𝙿 > 𝚅$ (we have both to start with a peak and to finish with a peak)