5.417. valley
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
A variable of the sequence of variables is a valley if and only if there exists an (with ) such that and and . is the total number of valleys of the sequence of variables .
- Example
-
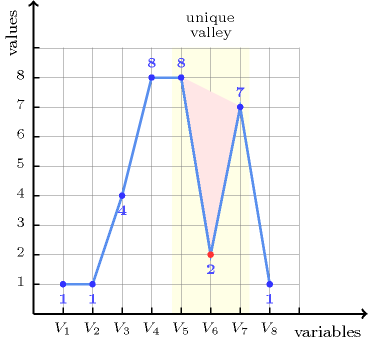
The first constraint holds since the sequence contains one valley that corresponds to the variable that is assigned to value 2.
Figure 5.417.1. Illustration of the first example of the Example slot: a sequence of eight variables , , , , , , , respectively fixed to values 1, 1, 4, 8, 8, 2, 7, 1 and its corresponding unique valley ()
- All solutions
Figure 5.417.2 gives all solutions to the following non ground instance of the constraint: , , , , , .
Figure 5.417.2. All solutions corresponding to the non ground example of the constraint of the All solutions slot where each valley is coloured in orange

- Typical
- Symmetries
- Arg. properties
Functional dependency: determined by .
Contractible wrt. when .
- Usage
Useful for constraining the number of valleys of a sequence of domain variables.
- Remark
Since the arity of the arc constraint is not fixed, the constraint cannot be currently described with the graph-based representation. However, this would not hold anymore if we were introducing a slot that specifies how to merge adjacent vertices of the final graph.
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 9 64 625 7776 117649 2097152 43046721 Number of solutions for : domains
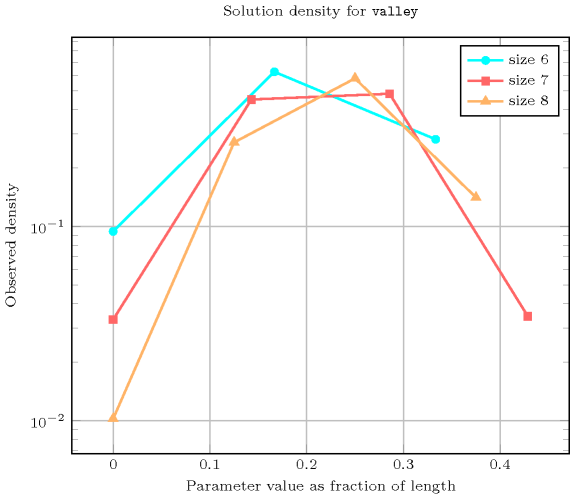
Length () 2 3 4 5 6 7 8 Total 9 64 625 7776 117649 2097152 43046721 Parameter value 0 9 50 295 1792 11088 69498 439791 1 - 14 330 5313 73528 944430 11654622 2 - - - 671 33033 1010922 24895038 3 - - - - - 72302 6057270 Solution count for : domains
- See also
common keyword: , , , (sequence).
generalisation: (a tolerance parameter is added for counting only big valleys).
related: , , , , .
specialisation: (the variable counting the number of valleys is set to 0 and removed).
- Keywords
characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.
combinatorial object: sequence.
constraint arguments: reverse of a constraint, pure functional dependency.
constraint network structure: sliding cyclic(1) constraint network(2).
- Cond. implications
- Automaton
Figure 5.417.3 depicts the automaton associated with the constraint. To each pair of consecutive variables of the collection corresponds a signature variable . The following signature constraint links , and : .
Figure 5.417.3. Automaton of the constraint
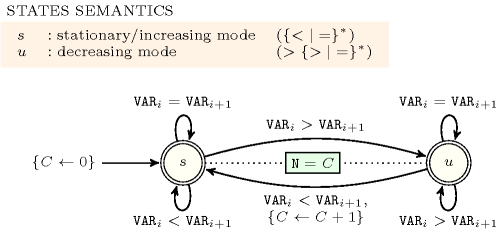
Figure 5.417.4. Hypergraph of the reformulation corresponding to the automaton of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )
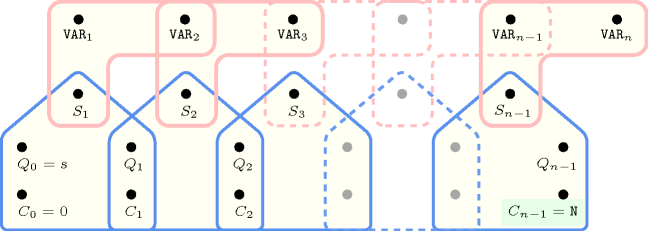
Figure 5.417.5. Glue matrix of the constraint
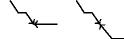
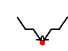

Figure 5.417.6. Illustrating the use of the state pair of the glue matrix for linking with the counters variables obtained after reading the prefix and corresponding suffix of the sequence ; note that the suffix (in pink) is proceed in reverse order; the left (resp. right) table shows the initialisation (for ) and the evolution (for ) of the state of the automaton and its counter upon reading the prefix (resp. the reverse suffix ).
