2.1.4. Explanation view

Given a constraint that cannot be satisfied the goal is to identify a smallest subset of variables and values for explaining that the constraint has no solution. Similarly, given a constraint that can be satisfied and a variable-value pair $(\mathrm{𝑣𝑎𝑟},\mathrm{𝑣𝑎𝑙})$ such that, if value $\mathrm{𝑣𝑎𝑙}$ is assigned to variable $\mathrm{𝑣𝑎𝑟}$ the constraint has no solution, the same question arises. Explanations are expressed in term of values that should be added to the domains of some variables in order to prevent unsatisfiability or filtering.

Figure 2.1.3. Illustration of the explanation why variable $V_2$ cannot be assigned value 3 for $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$$\left(\langle V_1,V_2,V_3,V_4,V_5,V_6,V_7,V_8\rangle \right)$ with $V_1\in [1,2]$, $V_2\in [1,3]$, $V_3\in [3,4]$, $V_4\in [3,5]$, $V_5\in [4,5]$, $V_6\in [6,7]$, $V_7\in [6,8]$, $V_8\in [8,9]$ wrt the maximum matching $M$ defined by $V_i=i$ ($1\le i\le 8$) and the corresponding digraph: (1) since adding any dotted green arc from $V_3$, $V_4$, $V_5$ to values 1 or 2 merges the strongly connected components containing $V_2$ and 3 this would prevent 3 from being removed from $V_2$; (2) since adding any dotted brown arc from $V_3$, $V_4$, $V_5$ to values 6, 7, 8 or 9 allows $V_3$ to reach the unmatched value 9 this would also prevent 3 from being removed from $V_2$.

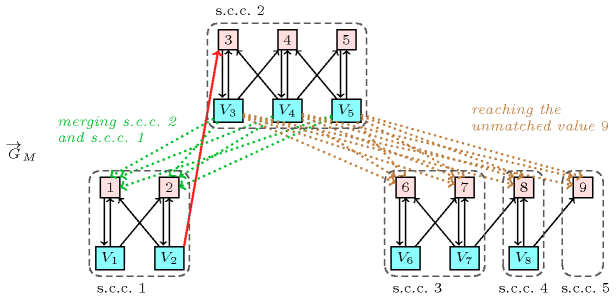
For the $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint Figure 2.1.3 provides the explanation attached to the instance described in Figure 2.1.1, i.e. what arcs should be added to prevent value 3 from being removed from the domain of variable $V_2$.