5.21. alldifferent_same_value
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
All the values assigned to the variables of the collection are pairwise distinct. is equal to number of constraints of the form that hold.
- Example
-
The constraint holds since:
All the values 7, 3, 1 and 5 are distinct,
Among the four expressions , , and exactly 2 conditions hold.
- Typical
- Symmetries
Items of and are permutable (same permutation used).
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Arg. properties
Functional dependency: determined by and .
- Usage
When all variables of the second collection are initially bound to distinct values the constraint can be explained in the following way:
We interpret the variables of the second collection as the previous solution to a problem where all variables have to be distinct.
We interpret the variables of the first collection as the current solution to find, where all variables should again be pairwise distinct.
The variable measures the of the current solution from the previous solution. This corresponds to the number of variables of that are assigned to the same previous value.
- See also
- Keywords
characteristic of a constraint: sort based reformulation, automaton, automaton with array of counters.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
The arc generator is used in order to generate all the arcs of the initial graph:
The arc generator creates all links between the items of the first collection ,
The arc generator creates a loop for each item of the second collection ,
Finally the arc generator creates an arc between items located at the same position in the collections and .
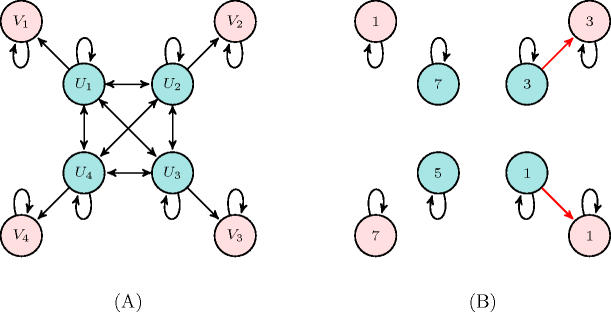
Part (A) of Figure 5.21.1 gives the initial graph associated with the Example slot. Variables of collection are coloured, while variables of collection are kept in white. Part (B) represents the final graph associated with the Example slot. In this graph each vertex constitutes a strongly connected component and the number of arcs that do not correspond to a loop is equal to 2 (i.e., ).
Figure 5.21.1. (A) Initial and (B) final graph of the , constraint with , , , and , , , (in Part (B) arcs in red correspond to the arcs counted by the argument )
- Automaton
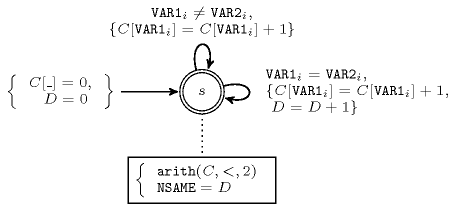
Figure 5.21.2 depicts the automaton associated with the constraint. Let and respectively denote the variables of the and collections. To each pair of variables corresponds a signature variable . The following signature constraint links , and : .
Figure 5.21.2. Automaton of the constraint