Proposition 68

Proof 68 (89) $n-1$ arcs are needed to connect $n$ $(n>1)$ vertices that all belong to a given connected component. Since we have two connected components, which respectively have $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices, this leads to the previous inequality. When $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ is equal to one we need an extra arc.

Proposition 69

Proof 69 If $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ are different then they correspond for sure to at least two distinct connected components.

Proposition 70

Proof 70 Since we have at least two distinct connected components, which respectively have $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices, this leads to the previous inequality.

Proposition 71

Proof 71 On the one hand, if $\mathrm{𝐍𝐂𝐂}\le 1$, we have that $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\le \mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$. On the other hand, if $\mathrm{𝐍𝐂𝐂}>1$, we have that $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\ge max(1,\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂})+\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ (i.e., $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\le \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-max(1,\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂})$). The result is obtained by taking the maximum value of the right-hand sides of the two inequalities.

Proposition 72

Proof 72 On the one hand, if $\mathrm{𝐍𝐂𝐂}\le 1$, we have that $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}\ge \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}$. On the other hand, if $\mathrm{𝐍𝐂𝐂}>1$, we have that $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}+max(1,\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂})\le \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}$ (i.e., $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}\le \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-max(1,\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂})$). The result follows.

Proposition 73

Proof 73 On the one hand, if $\mathrm{𝐍𝐂𝐂}\le 1$, we have that $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\le \mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$. On the other hand, if $\mathrm{𝐍𝐂𝐂}>1$, we have that $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\ge \mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}+\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$. Since $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}\le \mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}+\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ the result follows.

Proposition 74

Proof 74 We make the proof for $k\in \mathbb{N}$ (the interval $[k_{\mathrm{𝑖𝑛𝑓}},k_{\mathrm{𝑠𝑢𝑝}}]$ is only used for restricting the number of intervals to check). We have that $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\in [k·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂},k·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}]$. A forbidden interval $[k·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}+1,(k+1)·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}-1]$ corresponds to an interval between the end of interval $[k·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂},k·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}]$ and the start of the next interval $\left[\right(k+1)·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂},(k+1)·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}]$. Since all intervals $[i·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂},i·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}]$ $(i<k)$ end before $k·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ and since all intervals $[j·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂},j·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}]$ $(j>k)$ start after $(k+1)·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$, they do not use any value in $[k·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}+1,(k+1)·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}-1]$.

Proposition 75

Proof 75 On the one hand, (97) holds since the maximum number of arcs is achieved by taking $\mathrm{𝐍𝐂𝐂}$ connected components where each connected component is a clique involving $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices. On the other hand, (98) holds since a tree of $n$ vertices has $n-1$ arcs.

Proposition 76

Proof 76 The minimum number of arcs is achieved by taking one connected component with $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}-1$ arcs as well as $\mathrm{𝐍𝐂𝐂}-1$ connected components with a single vertex and a loop.

Proposition 77

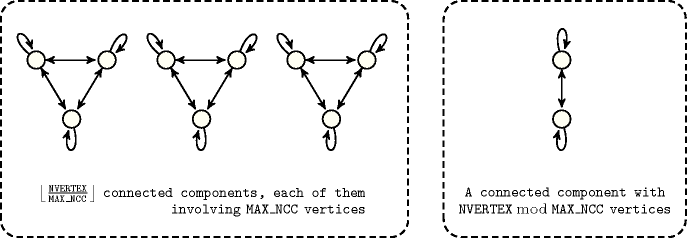
Proof 77 If $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}=0$ we get $\mathrm{𝐍𝐀𝐑𝐂}\le 0$ which holds since the set of vertices is empty. We now assume that $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}>0$. We first begin with the following claim:

let $G$ be a graph such that $V\left(G\right)-\mathrm{𝐍𝐂𝐂}(G,\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}(G\left)\right)*\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)\ge \mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$, then there exists a graph $G^{\text{'}}$ such that $V\left(G^{\text{'}}\right)=V\left(G\right)$, $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$, $\mathrm{𝐍𝐂𝐂}(G^{\text{'}},\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right))=\mathrm{𝐍𝐂𝐂}(G,\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right))+1$ and $\left|E\left(G\right)\right|\le |E\left(G^{\text{'}}\right)|$.

Proof of the claim

Let ${\left(C_i\right)}_{i\in \left[n\right]}$ be the connected components of $G$ on less than $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$ vertices and such that $|C_i|\ge |C_{i+1}|$. By hypothesis there exists $k\le n$ such that $|{\bigcup }_{i=1}^{k-1}{C}_i|<\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$ and $|{\bigcup }_{i=1}^k{C}_i|\ge \mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$.

• Either $|{\bigcup }_{i=1}^k{C}_i|=\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$, and then with $G^{\text{'}}$ such that $G^{\text{'}}$ restricted to the ${\bigcup }_{i=1}^k{C}_i$ be a complete graph and $G^{\text{'}}$ restricted to $V\left(G\right)-{\bigcup }_{i=1}^k{C}_i$ being exactly $G$ restricted to $V\left(G\right)-{\bigcup }_{i=1}^k{C}_i$ we obtain the claim.

• Or $|{\bigcup }_{i=1}^k{C}_i|>\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$. Then $C_k=C_k^1\uplus C_k^2$ such that $|\left({\bigcup }_{i=1}^{k-1}{C}_i\right)\cup C_k^1|=\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$ and $|C_k^2|<|C_1|$ (notice that $k\ge 2$). Then with $G^{\text{'}}$ such that $G^{\text{'}}$ restricted to $\left({\bigcup }_{i=1}^{k-1}{C}_i\right)\cup C_k^1$ is a complete graph and $G^{\text{'}}$ restricted to $V\left(G\right)-(\left({\bigcup }_{i=1}^{k-1}{C}_i\right)\cup C_k^1)$ is exactly $G$ restricted to $V\left(G\right)-(\left({\bigcup }_{i=1}^{k-1}{C}_i\right)\cup C_k^1)$ we obtain the claim.

End of proof of the claim

We prove by induction on $r\left(G\right)=⌊\frac{\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)}{\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)}⌋-\mathrm{𝐍𝐂𝐂}(G,\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right))$, where $G$ is any graph. For $r\left(G\right)=0$ the result holds (see Prop 44). Otherwise, since $r\left(G\right)>0$ we have that $V\left(G\right)-\mathrm{𝐍𝐂𝐂}(G,\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}(G\left)\right)*\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)\ge \mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}\left(G\right)$, by the previous claim there exists $G^{\text{'}}$ with the same number of vertices and the same number of vertices in the largest connected component, such that $r\left(G^{\text{'}}\right)=r\left(G\right)-1$. Consequently the result holds by induction.

Proposition 78

Proof 78 Let $G$ be a graph, let $X$ be a maximal size connected component of $G$, then we have $G=G\left[X\right]\oplus G\left[V\right(G)-X]$. On the one hand, as $G\left[X\right]$ is connected, by setting $\mathrm{𝐍𝐂𝐂}=1$ in 143 of Proposition 99, we have $\left|E\right(G\left[X\right])\ge |X|-1$, on the other hand, by Proposition 52, $\left|E\left(G[V\left(G\right)-X]\right)\right|\ge ⌈\frac{\left|V\right(G)-X|}{2}⌉$. Thus the result follows.

Proposition 79

Proof 79 Since a connected component contains at most $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices and since it does not contain any isolated vertex a connected component involves at most $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}-1$ sinks. Thus the result follows.

Proposition 80

Proof 80 Similar to Proposition 79.

Proposition 81

Proof 81 The number of vertices is less than or equal to the number of connected components multiplied by the largest number of vertices in a connected component.

Proposition 82

Proof 82 (105) The minimum number of vertices according to a fixed number of connected components $\mathrm{𝐍𝐂𝐂}$ such that one of the connected components contains $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices is obtained as follows: we get $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices from the connected component involving $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices and one vertex for each remaining connected component.

Proposition 83

Proof 83 (107) In a strongly connected component at least one arc has to leave each arc. Since we have two strongly connected components, which respectively have $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices, this leads to the previous inequality.

Proposition 84

Proof 84 Follows from the definitions of $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ and of $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$.

Proposition 85

Proof 85 Since we have at least two distinct strongly connected components, which respectively have $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices, this leads to the previous inequality.

Proposition 86

Proof 86 Similar to Proposition 74.

Proposition 87

Proof 87 The largest number of vertices is obtained by putting within each connected component the number of vertices of the largest strongly connected component.

Proposition 88

Proof 88 Since each strongly connected component contains at most $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices the total number of vertices is less than or equal to $\mathrm{𝐍𝐒𝐂𝐂}·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$.

Proposition 89

Proof 89 (114) The minimum number of vertices according to a fixed number of strongly connected components $\mathrm{𝐍𝐒𝐂𝐂}$ such that one of them contains $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices is equal to $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}+max(0,\mathrm{𝐍𝐒𝐂𝐂}-1)$.

Proposition 90

Proof 90 (116) The maximum number of vertices according to a fixed number of vertices $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}$ and to the fact that there is a connected component with $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ vertices is obtained by:

• Building a connected component with $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ vertices and creating an arc between each pair of vertices.

• Building a connected component with all the $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ remaining vertices and creating an arc between each pair of vertices.

Proposition 91

Proof 91 Achieving the minimum number of arcs with a fixed number of vertices and with a minimum number of vertices greater than or equal to one in each connected component is achieved in the following way:

• Since the minimum number of arcs of a connected component of $n$ vertices is $n-1$, splitting a connected component into $k$ parts that all have more than one vertex saves $k-1$ arcs. Therefore we build a maximum number of connected components. Since each connected component has at least $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ vertices we get $⌊\frac{\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}}{\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}}⌋$ connected components.

• Since we cannot build a connected component with the rest of the vertices (i.e., $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\mathrm{mod}\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ vertices left) we have to incorporate them in the previous connected components and this costs one arc for each vertex.

Proposition 92

Proof 92 The smallest number of vertices is obtained by taking all connected components to their minimum number of vertices $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$.

Proposition 93

Proof 93 If all vertices do not fit within the smallest connected component then we have at least two connected components.

Proposition 94

Proof 94 Achieving the maximum number of arcs, provided that we have at least one strongly connected component with $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices, is done by:

• Building a first strongly connected component ${𝒞}_1$ with $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices and adding an arc between each pair of vertices of ${𝒞}_1$.

• Building a second strongly connected component ${𝒞}_2$ with $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices and adding an arc between each pair of vertices of ${𝒞}_2$.

Finally, we add an arc from every vertex of ${𝒞}_1$ to every vertex of ${𝒞}_2$. This leads to a total number of arcs of $\mathrm{𝐌𝐈𝐍}\_{\mathrm{𝐍𝐒𝐂𝐂}}^2+{(\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂})}^2+\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}·(\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂})$.

Proposition 95

Proof 95 The smallest number of vertices is obtained by putting within each connected component the number of vertices of the smallest strongly connected component.

Proposition 96

Proof 96 Since each strongly connected component contains at least $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ vertices the total number of vertices is greater than or equal to $\mathrm{𝐍𝐒𝐂𝐂}·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$.

Proposition 97

Proof 97 If all vertices do not fit within the smallest strongly connected component then we have at least two strongly connected components.

Proposition 98

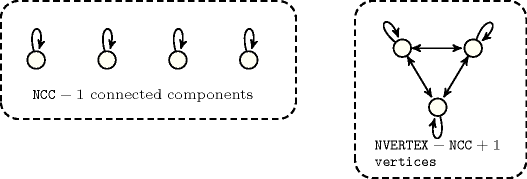
Proof 98 (133) We proceed by induction on $T\left(G\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-\left|X\right|-\left(\mathrm{𝐍𝐂𝐂}\right(G)-1)$, where $X$ is any connected component of $G$ of maximum cardinality. For $T\left(G\right)=0$ then either $\mathrm{𝐍𝐂𝐂}\left(G\right)=1$ and thus the formula is clearly true, or all the connected components of $G$, but possibly $X$, are reduced to one element. Since isolated vertices are not allowed, the formula holds.

Assume that $T\left(G\right)\ge 1$. Then there exists $Y$, a connected component of $G$ distinct from $X$, with more than one vertex. Let $y\in Y$ and let $G^{\text{'}}$ be the graph such that $V\left(G^{\text{'}}\right)=V\left(G\right)$ and $E\left(G^{\text{'}}\right)$ is defined by:

• For all $Z$ connected components of $G$ distinct from $X$ and $Y$ we have $G^{\text{'}}\left[Z\right]=G\left[Z\right]$.

• With $X^{\text{'}}=X\cup \left\{y\right\}$ and $Y^{\text{'}}=Y-\left\{y\right\}$, we have $G^{\text{'}}\left[Y^{\text{'}}\right]=G\left[Y^{\text{'}}\right]$ and $E\left(G^{\text{'}}\left[X^{\text{'}}\right]\right)=E\left(G\left[X\right]\right)\cup \left({\bigcup }_{x\in X^{\text{'}}}\{(x,y),(y,x)\}\right)$.

Clearly $|E\left(G^{\text{'}}\right)|-|E\left(G\right)|\ge 2·|X|+1-(2·\left|Y\right|-1)$ and since $X$ is of maximal cardinality the difference is strictly positive. Now as $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)$, $\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐂𝐂}\left(G\right)$ and as $T\left(G^{\text{'}}\right)=T\left(G\right)-1$ the result holds by induction hypothesis.

Proposition 99

Proof 99 (143) By induction of the number of vertices. The formula holds for one vertex. Let $G$ a graph with $n+1$ vertices $(n\ge 1)$. First assume there exists $x$ in $G$ such that $G-x$ has the same number of connected components than $G$. Since $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \mathrm{𝐍𝐀𝐑𝐂}(G-x)+1$, and by induction hypothesis $\mathrm{𝐍𝐀𝐑𝐂}(G-x)\ge \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}(G-x)-\mathrm{𝐍𝐂𝐂}(G-x)$ the result holds. Otherwise all connected components of $G$ are reduced to one vertex and the formula holds.

Proposition 100

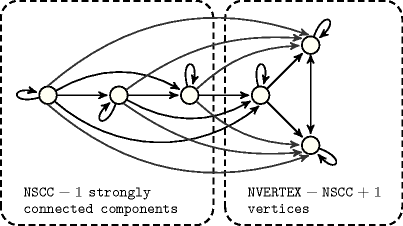
Proof 100 For proving 145, it is easier to rewrite the formula as $\mathrm{𝐍𝐀𝐑𝐂}\le {(\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-(\mathrm{𝐍𝐒𝐂𝐂}-1))}^2+(\mathrm{𝐍𝐂𝐂}-1)·(\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-(\mathrm{𝐍𝐒𝐂𝐂}-1))+\frac{\mathrm{𝐍𝐒𝐂𝐂}·(\mathrm{𝐍𝐒𝐂𝐂}-1)}{2}$. We proceed by induction on $T\left(G\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-\left|X\right|-\left(\mathrm{𝐍𝐒𝐂𝐂}\right(G)-1)$, where $X$ is any strongly connected component of $G$ of maximum cardinality.

For $T\left(G\right)=0$ then either $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)=1$ and thus the formula is clearly true, or all the strongly connected components of $G$, but possibly $X$, are reduced to one element. Since the maximum number of arcs in a directed acyclic graph of $n$ vertices is $\frac{n·(n+1)}{2}$, and as the subgraph of $G$ induced by all the strongly connected components of $G$ excepted $X$ is acyclic, the formula clearly holds.

Assume that $T\left(G\right)\ge 1$, let ${\left(X_i\right)}_{i\in I}$ be the family of strongly connected components of $G$, and let $G_r$ be the reduced graph of $G$ induced by ${\left(X_i\right)}_{i\in I}$ (that is $V\left(G_r\right)=I$ and $\forall i_1,i_2\in I$, $(i_1,i_2)\in E\left(G_r\right)$ if and only if $\exists x_1\in X_{i_1}$, $\exists x_2\in X_{i_2}$ such that $(x_1,x_2)\in E$). Consider $G^{\text{'}}$ such that $V\left(G^{\text{'}}\right)=V\left(G\right)$ and $E\left(G^{\text{'}}\right)$ is defined by:

• For all strongly connected components $Z$ of $G$ we have $G^{\text{'}}\left[Z\right]=G\left[Z\right]$.

• For $\sigma$ be any topological sort of $G_r$, $\forall x_i\in X_i$, $\forall x_j\in X_j$, $(x_i,x_j)\in E\left(G^{\text{'}}\right)$ whenever $i$ is less than $j$ with respect to $\sigma$.

Notice that $G^{\text{'}}$ satisfies the following properties: $T\left(G^{\text{'}}\right)=T\left(G\right)$, $V\left(G^{\text{'}}\right)=V\left(G\right)$, $\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)$, $E\left(G\right)\subseteq E\left(G^{\text{'}}\right)$, ${\left(X_i\right)}_{i\in I}$ is still the family of strongly connected components of $G^{\text{'}}$, and moreover, for every $i\in I$ and every $x_i\in X_i$ we have that $x_i$ is connected to any vertex outside $X_i$, that is the number of arcs incident to $x_i$ and incident to vertices outside $X_i$ is exactly $|V\left(G^{\text{'}}\right)|-|X_i|$.

Now, as $T\left(G^{\text{'}}\right)\ge 1$, there exists $Y$, a strongly connected component of $G^{\text{'}}$ distinct from $X$, with more than one vertex. Let $y\in Y$ and let $G^{\text{'}\text{'}}$ be the graph such that $V\left(G^{\text{'}\text{'}}\right)=V\left(G^{\text{'}}\right)$ and $E\left(G^{\text{'}\text{'}}\right)$ is defined by:

• $G^{\text{'}\text{'}}[V\left(G\right)-\left\{y\right\}]=G^{\text{'}}[V\left(G\right)-\left\{y\right\}]$.

• With $X^{\text{'}}=X\cup \left\{y\right\}$, we have $G^{\text{'}\text{'}}\left[Y^{\text{'}}\right]=G^{\text{'}}\left[Y^{\text{'}}\right]$ and $E\left(G^{\text{'}\text{'}}\left[X^{\text{'}}\right]\right)=E\left(G^{\text{'}}\left[X\right]\right)\cup \left({\bigcup }_{x\in X^{\text{'}}}\{(x,y),(y,x)\}\right)$.

• Assume that $X=X_j$ for $j\in I$. Then $\forall i\in I-\left\{j\right\}$, $\forall x_i\in X_i$, $(x_i,y)\in E\left(G^{\text{'}\text{'}}\right)$ whenever $i$ is less than $j$ with respect to $\sigma$ and $(y,x_i)\in E\left(G^{\text{'}\text{'}}\right)$ whenever $j$ is less than $i$ with respect to $\sigma$.

Clearly $|E\left(G^{\text{'}\text{'}}\right)|-|E\left(G^{\text{'}}\right)|\ge 2|X|+1+|V\left(G^{\text{'}}\right)|-|X|-(2·\left|Y\right|-1+|V\left(G^{\text{'}}\right)|-|Y\left|\right)=\left|X\right|-\left|Y\right|+2$ and since $X$ is of maximal cardinality the difference is strictly positive. As $E\left(G\right)\subseteq E\left(G^{\text{'}}\right)$, $|E\left(G^{\text{'}\text{'}}\right)|-|E\left(G\right)|$ is also strictly positive. Now as $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}\text{'}}\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)$, $\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}\text{'}}\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)$ and as $T\left(G^{\text{'}\text{'}}\right)=T\left(G^{\text{'}}\right)-1=T\left(G\right)-1$ the result holds by induction hypothesis.

Proposition 101

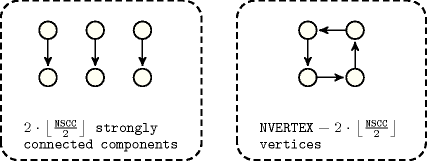
Proof 101 For proving part 147 of Proposition 101 we proceed by induction on $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)$. If $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)=1$ then, we have $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)$ (i.e., for one vertex this is true since every vertex has at least one arc, otherwise every vertex $v$ has an arc arriving on $v$ as well as an arc starting from $v$, thus we have $\mathrm{𝐍𝐀𝐑𝐂}\ge \frac{2·\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}}{2}$). If $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)>1$ let $X$ be a strongly connected component of $G$. Then $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \mathrm{𝐍𝐀𝐑𝐂}\left(G\right[V\left(G\right)-X\left]\right)+\mathrm{𝐍𝐀𝐑𝐂}\left(G\right[X\left]\right)$. By induction hypothesis $\mathrm{𝐍𝐀𝐑𝐂}\left(G[V\left(G\right)-X]\right)\ge |V\left(G\right)-X|-⌊\frac{\mathrm{𝐍𝐒𝐂𝐂}\left(G\right[V\left(G\right)-X\left]\right)-1}{2}⌋$, thus $\mathrm{𝐍𝐀𝐑𝐂}\left(G[V\left(G\right)-X]\right)\ge |V\left(G\right)-X|-⌊\frac{\left(\mathrm{𝐍𝐒𝐂𝐂}\right(G)-1)-1}{2}⌋$. Since $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right[X\left]\right)\ge \left|X\right|$ we obtain $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \left|V\left(G\right)\right|-⌊\frac{\left(\mathrm{𝐍𝐒𝐂𝐂}\right(G)-1)-1}{2}⌋$, and thus the result holds.

Proposition 102

Proof 102 As shown in [BessiereHebrardHnichKiziltanWalsh05], a lower bound for the minimum number of equivalence classes (e.g., strongly connected components) is the independence number of the graph and the right-hand side of Proposition 102 corresponds to a lower bound of the independence number proposed by Turán [Turan41].

Proposition 103

Proof 103 See [Hansen75] and [FavaronMaheoSacle88].

Proposition 104

Proof 104 The maximum number of arcs is achieved by the following pattern: for all non-sink vertices we have an arc to all vertices.

Proposition 105

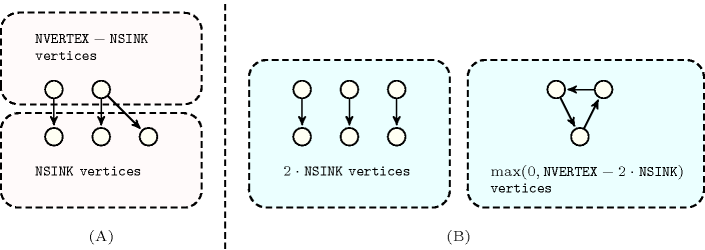
Proof 105 Recall that for $x\in V\left(G\right)$, we have that $d_G^{+}\left(x\right)+d_G^{-}\left(x\right)\ge 1$. If $x$ is a sink then $d_G^{-}\left(x\right)\ge 1$, consequently $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \mathrm{𝐍𝐒𝐈𝐍𝐊}\left(G\right)$. If $x$ is not a sink then $d_G^{+}\left(x\right)\ge 1$, consequently $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \left|V\right(G\left)\right|-\mathrm{𝐍𝐒𝐈𝐍𝐊}\left(G\right)$.

Proposition 106

Proof 106 The maximum number of arcs is achieved by the following pattern: for all non-source vertices we have an arc from all vertices.

Proposition 107

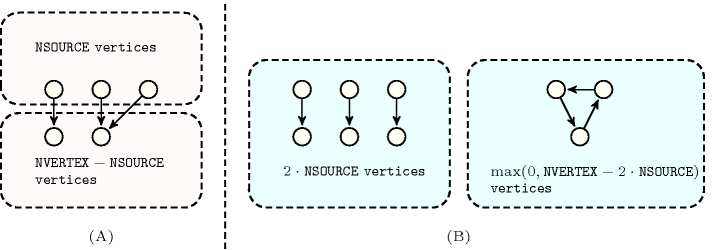
Proof 107 Similar to Proposition 105.

Proposition 108

Proof 108 Since sinks and sources cannot belong to a circuit and since they cannot coincide (i.e., because isolated vertices are not allowed) the result follows.

Proposition 109

Proof 109 No vertex can be both a source and a sink (isolated vertices are removed).