Proposition 110 Let $\alpha$ denote $max(0,\mathrm{𝐍𝐂𝐂}-1)$.

Proof 110 We construct $\mathrm{𝐍𝐂𝐂}-1$ connected components with $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices and one connected component with $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ vertices. $n^2$ corresponds to the maximum number of arcs in a connected component. $n$, $2·n-2$, $\frac{n·(n+1)}{2}$, $\frac{n·(n+1)}{2}$, $\frac{n·(n-1)}{2}$, $\frac{n·(n-1)}{2}$, $n^2-n$, $2·n$ and $n-1$ respectively correspond to the maximum number of arcs in a connected component of $n$ vertices according to the fact that we use the arc generator $\mathrm{𝐶𝐼𝑅𝐶𝑈𝐼𝑇}$, $\mathrm{𝐶𝐻𝐴𝐼𝑁}$, $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}(\le )$ $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}(\ge )$ $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}(<)$ $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}(>)$ $\mathrm{𝐶𝐿𝐼𝑄𝑈𝐸}(\ne )$ $\mathrm{𝐶𝑌𝐶𝐿𝐸}$ or $\mathrm{𝑃𝐴𝑇𝐻}$.

Proposition 111

Proof 111 (165) We construct $\mathrm{𝐍𝐂𝐂}-1$ connected components with $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ vertices and one connected component with $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices. The quantity $max(1,n-1)$ corresponds to the minimum number of arcs in a connected component of $n$ $(n>0)$ vertices.

Proposition 112

Proof 112 Derived from the definitions of $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$.

Proposition 113

Proof 113 Derived from the definitions of $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$.

Proposition 114

Proof 114 Since a connected component contains at most $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}$ vertices and since it does not contain any isolated vertex and since a same vertex cannot be both a sink and a source a connected component involves at most $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}-1$ sinks and sources all together. Thus the result follows.

Proposition 115

Proof 115 We assume that we have at least two strongly connected components (the case with one being obvious). Let ${\left(SC{C}_i\right)}_{i\in \left[\mathrm{𝐍𝐂𝐂}\right(G\left)\right]}$ be the family of strongly connected components of $G$. Then $\left|E\left(G\right)\right|\le {\sum }_{i\in \left[\mathrm{𝐍𝐂𝐂}\right(G\left)\right]}\left|E\left(G\left[SC{C}_i\right]\right)\right|+k$, where $k$ is the number of arcs between the distinct strongly connected components of $G$. For any strongly connected component $SC{C}_i$ the number of arcs it has with the other strongly connected components is bounded by $|SC{C}_i|·(|V\left(G\right)-SC{C}_i\left|\right)$. Consequently, $k\le \frac{1}{2}·{\sum }_{i\in \left[\mathrm{𝐍𝐂𝐂}\right(G\left)\right]}|SC{C}_i|·(|V\left(G\right)-SC{C}_i\left|\right)$. W.l.o.g. we assume $|SC{C}_1|=\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$. Then we get $k\le \frac{1}{2}·(\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}·(\mathrm{𝐍𝐂𝐂}-1)·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}+\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}·((\mathrm{𝐍𝐂𝐂}-2)·\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐂𝐂}+\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}))$.

Proposition 116

Proof 116 Let ${\left(SC{C}_i\right)}_{i\in \left[\mathrm{𝐍𝐂𝐂}\right(G\left)\right]}$ be the family of strongly connected components of $G$, as $\left|E\left(G\right)\right|\ge {\sum }_{i\in \left[\mathrm{𝐍𝐂𝐂}\right(G\left)\right]}\left|E\left(G\left[SC{C}_i\right]\right)\right|$, we obtain the result since in a strongly connected graph the number of edges is at least its number of vertices.

Proposition 117

Proof 117 Derived from the definitions of $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$.

Proposition 118

Proof 118 Derived from the definitions of $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐒𝐂𝐂}$ and $\mathrm{𝐌𝐀𝐗}\_\mathrm{𝐍𝐒𝐂𝐂}$.

Proposition 119 Let $\alpha$, $\beta$ and $\gamma$ respectively denote $max(0,\mathrm{𝐍𝐂𝐂}-1)$, $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}-\alpha ·\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$ and $\mathrm{𝐌𝐈𝐍}\_\mathrm{𝐍𝐂𝐂}$.

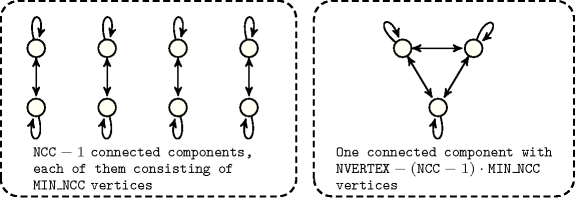
Proof 119 For proving inequality 174 we proceed by induction on the number of vertices of $G$. First note that if all the connected components are reduced to one element the result is obvious. Thus we assume that the number of vertices in the maximal sized connected component of $G$ is at least 2. Let $x$ be an element of the maximal sized connected component of $G$. Then, $G-x$ satisfies $\alpha (G-x)=\alpha \left(G\right)$, $\gamma (G-x)=\gamma \left(G\right)$ and $\beta (G-x)=\beta \left(G\right)-1$. Since by induction hypothesis $\left|E(G-x)\right|\le \alpha (G-x)·\gamma {(G-x)}^2+\beta {(G-x)}^2$, and since the number of arcs of $G$ incident to $x$ is at most $2·\left(\beta \right(G)-1)+1$, we have that $\left|E\left(G\right)\right|\le \alpha \left(G\right)·\gamma {\left(G\right)}^2+{(\beta \left(G\right)-1)}^2+2·(\beta \left(G\right)-1)+1$. And thus the result follows.

Proposition 120

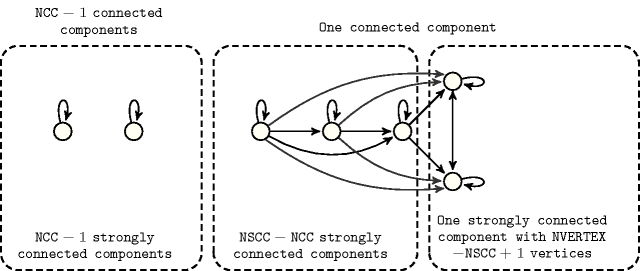
Proof 120 We proceed by induction on $T\left(G\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-\left|X\right|-\left(\mathrm{𝐍𝐂𝐂}\right(G)-1)$, where $X$ is any connected component of $G$ of maximum cardinality. For $T\left(G\right)=0$ then either $\mathrm{𝐍𝐂𝐂}\left(G\right)=1$ and thus the formula is clearly true, by Proposition 145 or all the connected components of $G$, but possibly $X$, are reduced to one element. Since isolated vertices are not allowed, again by Proposition 145 applied on $G\left[X\right]$, the formula holds indeed $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right[X\left]\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-\left(\mathrm{𝐍𝐂𝐂}\right(G)-1)$ and $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right[X\left]\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)-\left(\mathrm{𝐍𝐂𝐂}\right(G)-1)$.

Assume that $T\left(G\right)\ge 1$. Then there exists $Y$, a connected component of $G$ distinct from $X$, with more than one vertex.

• Firstly assume that $G\left[Y\right]$ is strongly connected. Let $y\in Y$ and let $G^{\text{'}}$ be the graph such that $V\left(G^{\text{'}}\right)=V\left(G\right)$ and $E\left(G^{\text{'}}\right)$ is defined by:

  • For all $Z$ connected components of $G$ distinct from $X$ and $Y$ we have $G^{\text{'}}\left[Z\right]=G\left[Z\right]$.

  • With $X^{\text{'}}=X\cup (Y-\left\{y\right\})$ and $Y^{\text{'}}=\left\{y\right\}$, we have $E\left(G^{\text{'}}\left[Y^{\text{'}}\right]\right)=\left\{(y,y)\right\}$, $E\left(G^{\text{'}}\left[X^{\text{'}}\right]\right)=E\left(G\left[X\right]\right)\cup \{(z,x):z\in Y-\left\{y\right\},x\in X\}\cup \{(z,t):z,t\in Y-\left\{y\right\}\}$.

  Clearly we have that $|E\left(G^{\text{'}}\right)|-|E\left(G\right)|\ge (\left|Y\right|-1)·|X|-2·(\left|Y\right|-1)$ and since $\left|X\right|\ge \left|Y\right|\ge 2$, the difference is positive or null. Now as $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)$, $\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐂𝐂}\left(G\right)$, $\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)$ (since $G^{\text{'}}[Y-\left\{y\right\}]$ is strongly connected because $E\left(G^{\text{'}}[Y-\left\{y\right\}]\right)=\{(z,t):z,t\in Y-\left\{y\right\}\}$ and since the reduced graph of the strongly connected components of $G^{\text{'}}\left[X^{\text{'}}\right]$ is exactly the reduced graph of the strongly connected components of $G\left[X\right]$ to which a unique source has been added) and as $T\left(G^{\text{'}}\right)\le T\left(G\right)-1$, the result holds by induction hypothesis.

• Secondly assume that $G\left[Y\right]$ is not strongly connected. Let $Z\subset Y$ such that $Z$ is a strongly connected component of $G\left[Y\right]$ corresponding to a source in the reduced graph of the strongly connected components of $G\left[Y\right]$. Let $G^{\text{'}}$ be the graph such that $V\left(G^{\text{'}}\right)=V\left(G\right)$ and $E\left(G^{\text{'}}\right)$ is defined by:

  • For all $W$ connected components of $G$ distinct from $X$ and $Y$ we have $G^{\text{'}}\left[W\right]=G\left[W\right]$.

  • With $X^{\text{'}}=X\cup Z$ and $Y^{\text{'}}=Y-Z$, we have $E\left(G^{\text{'}}\left[Y^{\text{'}}\right]\right)=E\left(G\left[Y^{\text{'}}\right]\right)$ if $|Y^{\text{'}}|>1$ and $E\left(G^{\text{'}}\left[Y^{\text{'}}\right]\right)=\left\{(y,y)\right\}$ if $Y^{\text{'}}=\left\{y\right\}$. $E\left(G^{\text{'}}\left[X^{\text{'}}\right]\right)=E\left(G\left[X\right]\right)\cup \{(z,x):z\in Z,x\in X\}$.

  Clearly we have that $|E\left(G^{\text{'}}\right)|-|E\left(G\right)|\ge |Z|·|X|-|Z|·(\left|Y\right|-\left|Z\right|)$ and since $\left|X\right|>\left|Y\right|-\left|Z\right|$, the difference is strictly positive. Now as $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)$, $\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐂𝐂}\left(G\right)$, $\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)$ and as $T\left(G^{\text{'}}\right)\le T\left(G\right)-1$, the result holds by induction hypothesis.

Proposition 121

Proof 121 We prove that the invariant is valid for any digraph $G$. First notice that for an operational behaviour, since we cannot assume that Proposition 55 (i.e., $\mathrm{𝐍𝐂𝐂}\left(G\right)\le \mathrm{𝐍𝐒𝐂𝐂}\left(G\right)$) was already triggered, we use the $max$ operator. But since any strongly connected component is connected, then $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)-\mathrm{𝐍𝐂𝐂}\left(G\right)$ is never negative. Consequently we only show by induction on $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)$ that $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-min\left(\mathrm{𝐍𝐂𝐂}\right(G),\mathrm{𝐍𝐒𝐂𝐂}(G)-\mathrm{𝐍𝐂𝐂}(G\left)\right)$. To begin notice that if $X$ is a strongly (non void) connected component then either $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right[X\left]\right)\ge \left|X\right|$ or $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right[X\left]\right)=0$ and in this latter case we have that both $\left|X\right|=1$ and $X$ is strictly included in a connected component of $G$ (recall that isolated vertices are not allowed). Thus we can directly assume that $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)=k>1$.

First, consider that there exists a connected component of $G$, say $X$, which is also strongly connected. Let $G^{\text{'}}=G-X$, consequently we have $\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)-1$, $\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐂𝐂}\left(G\right)-1$, $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-\left|X\right|$, and $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \left|X\right|+\mathrm{𝐍𝐀𝐑𝐂}\left(G^{\text{'}}\right)$. Then $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \left|X\right|+\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)-min(\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right),\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)-\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right))$ and thus $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-min\left(\mathrm{𝐍𝐂𝐂}\right(G)-1,\mathrm{𝐍𝐒𝐂𝐂}(G)-\mathrm{𝐍𝐂𝐂}(G\left)\right)$, which immediately gives the result.

Second consider that any strongly connected component is strictly included in a connected component of $G$. Then, either there exists a strongly connected component $X$ such that $\left|X\right|\ge 2$. Let $G^{\text{'}}=G-X$, consequently we have $\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)-1$, $\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐂𝐂}\left(G\right)$, $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-\left|X\right|$, and $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \left|X\right|+1+\mathrm{𝐍𝐀𝐑𝐂}\left(G^{\text{'}}\right)$. Then $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \left|X\right|+1+\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G^{\text{'}}\right)-min(\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right),\mathrm{𝐍𝐒𝐂𝐂}\left(G^{\text{'}}\right)-\mathrm{𝐍𝐂𝐂}\left(G^{\text{'}}\right))$ and thus $\mathrm{𝐍𝐀𝐑𝐂}\left(G\right)\ge \mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)+1-min\left(\mathrm{𝐍𝐂𝐂}\right(G),\mathrm{𝐍𝐒𝐂𝐂}(G)-\mathrm{𝐍𝐂𝐂}(G)+1)$, which immediately gives the result. Or, all the strongly connected components are reduced to one element, so we have $\mathrm{𝐍𝐒𝐂𝐂}\left(G\right)=\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)$, and thus we obtain that $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}\left(G\right)-min\left(\mathrm{𝐍𝐂𝐂}\right(G),\mathrm{𝐍𝐒𝐂𝐂}(G)-\mathrm{𝐍𝐂𝐂}(G\left)\right)=min\left(\mathrm{𝐍𝐂𝐂}\right(G),\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}(G)-\mathrm{𝐍𝐂𝐂}(G\left)\right)$, which gives the result by for example Proposition 99 (143).

Proposition 122

Proof 122 Since the maximum number of arcs of a digraph is ${\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}}^2$, and since:

• No vertex can have a source as a successor we lose $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}·\mathrm{𝐍𝐒𝐎𝐔𝐑𝐂𝐄}$ arcs,

• No sink can have a successor we lose $\mathrm{𝐍𝐕𝐄𝐑𝐓𝐄𝐗}·\mathrm{𝐍𝐒𝐈𝐍𝐊}$ arcs.

In these two sets of arcs we count twice the arcs from the sinks to the sources, so we finally get a maximum number of arcs corresponding to the right-hand side of the inequality to prove.