3.7.153. Minimum cost flow

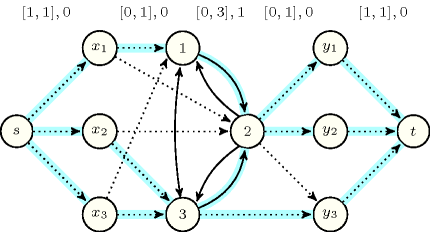
A constraint for which there is a filtering algorithm based on an algorithm that finds a minimum cost flow in a graph. This graph is usually constructed from the variables of the constraint as well as from their potential values. FigureΒ 3.7.42 illustrates the minimum cost flow model used for the 𝚜𝚘𝚏𝚝_πšœπšŠπš–πšŽ_πšŸπšŠπš› constraint. The demand and the capacity of the arcs are depicted by an interval on top of the corresponding arcs. The weight is given after that interval: a weight of 0 (respectively 1) is depicted by a dotted (respectively plain) arc. Weights of 1 are assigned to arcs linking two values since they model the correction of a discrepancy between variables x 1 , x 2 , x 3 and variables y 1 , y 2 , y 3 . Blue arcs represent the feasible flow corresponding to the solution 𝚜𝚘𝚏𝚝_πšœπšŠπš–πšŽ_πšŸπšŠπš›(2,〈1,3,3βŒͺ,〈2,2,3βŒͺ).

Figure 3.7.42. Minimum cost flow model for the 𝚜𝚘𝚏𝚝_πšœπšŠπš–πšŽ_πšŸπšŠπš› constraint described in TableΒ 3.7.42
ctrs/preface-182-tikz
Table 3.7.42. Domains of the variables for the 𝚜𝚘𝚏𝚝_πšœπšŠπš–πšŽ_πšŸπšŠπš› constraint of FigureΒ 3.7.42.
iπ‘‘π‘œπ‘š(x i )iπ‘‘π‘œπ‘š(y i )
1{1,2}1{2}
2{2,3}2{2}
3{1,3}3{2,3}