• $\mathrm{𝚎𝚕𝚎𝚖}$,

• $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$.

Some optimisation problems involve minimising a cost $c$ consisting of a sum of elementary costs $c_1,c_2,\cdots ,c_n$, where each elementary cost $c_i$ $(1\le i\le n)$ is directly linked to the value assigned to a decision variable $v_i$. Without loss of generality we assume that each decision variable will be assigned a value between 1 and $m$. The link between a decision variable $v_i$ and its corresponding cost $c_i$ is usually expressed by a constraint of the form $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$$(v_i,\langle c_{i,1},c_{i,2},\cdots ,c_{i,m}\rangle ,c_i)$ stating that $c_i=j\Rightarrow c_i=c_{i,j}$. During search, while enumerating on the different values of a decision variable $v_i$, we would like to try out values of $v_i$ so that the corresponding cost $c_i$ increases. This means we want to use a permutation ${\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_m$ of $1,2,\cdots ,m$ such that $c_{i,{\sigma }_1}\le c_{i,{\sigma }_2}\le \cdots \le c_{i,{\sigma }_m}$. Note that such permutation can be obtained by sorting the costs $c_{i,1},c_{i,2},\cdots ,c_{i,m}$ by increasing order and by collecting the position ${\sigma }_j$ where item $c_{i,j}$ is located in the sorted list. Assuming that we perform arc-consistency on the $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$, we now describe three different ways to obtain the effect we want to achieve:

• A first direct way is to use a built in facility that, given variable $v_i$ and the corresponding list of values ${\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_m$ introduced before, creates a choice point and tries to successively assign values ${\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_m$ to $v_i$. Note that, once $v_i$ is fixed there is no need to enumerate on the corresponding elementary cost variable $c_i$ since, by propagation, $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$$(v_i,\langle c_{i,1},c_{i,2},\cdots ,c_{i,m}\rangle ,c_i)$ will fix $c_i$. Consequently the cost variables do not need to be passed to the search procedure.

• A second indirect way, used when we want to only rely on a standard built in that creates a choice point and tries to assign values to a variable in increasing value order, is to introduce an extra variable $u_i$. The idea is to link variable $u_i$ to variable $v_i$ in such a way that, when we try to assign values in increasing value order to variable $u_i$, both variables $v_i$ and $c_i$ get fixed and, in addition, values of $c_i$ are increasing. This can be modelled by introducing the following two $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$ constraints:

  1. $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$$(u_i,\langle {\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_m\rangle ,v_i)$

  2. $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$$(v_i,\langle c_{i,1},c_{i,2},\cdots ,c_{i,m}\rangle ,c_i)$

  The effect of a dedicated built in that tries to assign values to a variable according to an explicit list of values is achieved by introducing the first $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$ constraint. Again, once $u_i$ is fixed the first $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$ constraint will fix variable $v_i$. Then the second $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$ constraint will also fix variable $c_i$. Consequently, both the cost and the decision variables do not need to be passed to the search procedure, i.e., we just need to pass the newly introduced variables $u_i$.

• Finally, we can first label on the cost variable $c_i$ in increasing value order. If the costs $c_{i,1},c_{i,2},\cdots ,c_{i,m}$ are all distinct then the $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$$(v_i,\langle c_{i,1},c_{i,2},\cdots ,c_{i,m}\rangle ,c_i)$ constraint will fix $v_i$ by propagation since we assume $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$ to perform arc-consistency. Otherwise, when the costs $c_{i,1},c_{i,2},\cdots ,c_{i,m}$ are not all distinct, we also need to label the decision variable $v_i$.

Figure 3.7.35. Given a decision variable $v$ and a corresponding cost variable $c$ linked by the $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$$(v,\langle 5,6,2,9,9\rangle ,c)$ constraint, illustration of three ways for labelling by increasing cost: part (A) labels directly on the decision variable $v$ using an appropriate order so that successive values of $c$ are increasing; part (B) introduces a variable $u$ linked to $v$ by the $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$$(u,\langle 3,1,2,4,5\rangle ,v)$ constraint and labels on $u$ by increasing value order; part (C) labels first on the cost variable $c$ by increasing value order, and then on variable $v$.

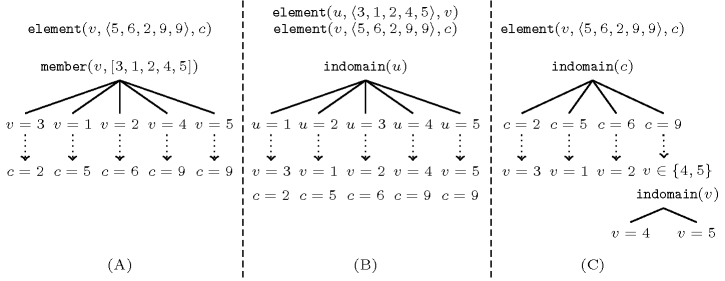
Figure 3.7.35 illustrates the three ways of labelling previously introduced. The primitive member$(\mathrm{𝑣𝑎𝑟},\mathrm{𝑙𝑖𝑠𝑡}\_\mathrm{𝑣𝑎𝑙𝑢𝑒𝑠})$ creates a choice point and tries to successively assign variable $\mathrm{𝑣𝑎𝑟}$ an integer value from the list $\mathrm{𝑙𝑖𝑠𝑡}\_\mathrm{𝑣𝑎𝑙𝑢𝑒𝑠}$ with respect to their ordering. The primitive indomain$\left(\mathrm{𝑣𝑎𝑟}\right)$ also creates a choice point and tries to successively assign variable $\mathrm{𝑣𝑎𝑟}$ an integer value of its domain, by increasing value order.