• $\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎}$.

A constraint that can use some filtering based on the longest closed and open hole problems  [BeldiceanuCarlssonPoder08]. We follow the presentation from the previous paper. Before presenting the longest closed open hole scheduling problems, let us first introduce some notation related to the $\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎}$$(\mathrm{𝚃𝙰𝚂𝙺𝚂},\mathrm{𝙻𝙸𝙼𝙸𝚃})$ constraint that will be used within the context of the longest closed and open hole problems.

Here, $\mathrm{𝚃𝙰𝚂𝙺𝚂}$ is a collection of tasks, and for a task $t\in \mathrm{𝚃𝙰𝚂𝙺𝚂}$, $t.\mathrm{𝚘𝚛𝚒𝚐𝚒𝚗}$, $t.\mathrm{𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗}$ and $t.\mathrm{𝚑𝚎𝚒𝚐𝚑𝚝}$ denote respectively its start, duration and height, while $\mathrm{𝙻𝙸𝙼𝙸𝚃}\in {\mathbb{Z}}^{+}$ is the height of the resource. The constraint is equivalent to finding an assignment $s:\mathrm{𝚃𝙰𝚂𝙺𝚂}.\mathrm{𝚘𝚛𝚒𝚐𝚒𝚗}\to {\mathbb{Z}}^{+}$Without loss of generality we assume the earliest start of each task to be greater than or equal to 0. that solves the cumulative placement of $\mathrm{𝚃𝙰𝚂𝙺𝚂}$ of maximum height $\mathrm{𝙻𝙸𝙼𝙸𝚃}$, i.e.:

where the coverage $P(\mathrm{𝚃𝙰𝚂𝙺𝚂},i)$ by $\mathrm{𝚃𝙰𝚂𝙺𝚂}$ of instant $i\in \mathbb{Z}$ is:

We are now in position to define the longest closed and open hole problems. Given a quantity $\sigma \in {\mathbb{Z}}^{+}$ of slack (i.e. the difference between the available space and the total area of the tasks to place), the longest closed hole problem is to find the largest integer ${\mathrm{𝑙𝑐𝑚𝑎𝑥}}_{\sigma }^{\mathrm{𝙻𝙸𝙼𝙸𝚃}}\left(\mathrm{𝚃𝙰𝚂𝙺𝚂}\right)$ for which there exists a cumulative placement $s$ of a subset of tasks ${\mathrm{𝚃𝙰𝚂𝙺𝚂}}^{\text{'}}\subseteq \mathrm{𝚃𝙰𝚂𝙺𝚂}$ of maximum height $\mathrm{𝙻𝙸𝙼𝙸𝚃}$, such that the resource area that is not occupied by $s$ on interval $[0,{\mathrm{𝑙𝑐𝑚𝑎𝑥}}_{\sigma }^{\mathrm{𝙻𝙸𝙼𝙸𝚃}})$ does not exceed the maximum allowed slack value $\sigma$:

The longest open hole problem is to find the largest integer ${\mathrm{𝑙𝑚𝑎𝑥}}_{\sigma }^{\mathrm{𝙻𝙸𝙼𝙸𝚃}}\left(\mathrm{𝚃𝙰𝚂𝙺𝚂}\right)$ for which there exists a cumulative placement $s$ of a subset of tasks ${\mathrm{𝚃𝙰𝚂𝙺𝚂}}^{\text{'}}\subseteq \mathrm{𝚃𝙰𝚂𝙺𝚂}$ of maximum height $\mathrm{𝙻𝙸𝙼𝙸𝚃}$ and an interval $[i^{\text{'}},i^{\text{'}}+{\mathrm{𝑙𝑚𝑎𝑥}}_{\sigma }^{\mathrm{𝙻𝙸𝙼𝙸𝚃}})\subset \mathbb{Z}$ of length ${\mathrm{𝑙𝑚𝑎𝑥}}_{\sigma }^{\mathrm{𝙻𝙸𝙼𝙸𝚃}}$, such that the resource area that is not occupied by $s$ on $[i^{\text{'}},i^{\text{'}}+{\mathrm{𝑙𝑚𝑎𝑥}}_{\sigma }^{\mathrm{𝙻𝙸𝙼𝙸𝚃}})$ does not exceed the maximum allowed slack value $\sigma$:

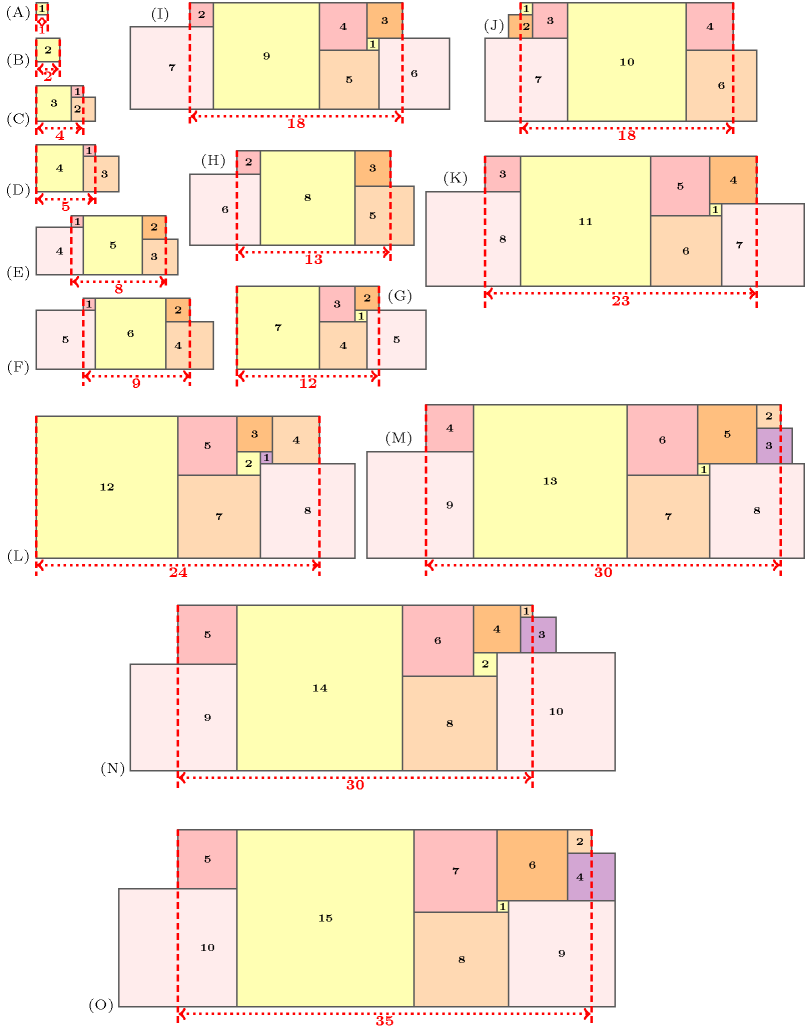
As an example, consider seven tasks of respective size $11\times 11$, $9\times 9$, $8\times 8$, $7\times 7$, $6\times 6$, $4\times 4$, $2\times 2$. Part (A) of Figure 3.7.20 provides a cumulative placement corresponding to the longest open hole problem according to $\mathrm{𝙻𝙸𝙼𝙸𝚃}=11$ and $\sigma =0$. The longest open hole ${\mathrm{𝑙𝑚𝑎𝑥}}_0^{11}\left(\{11\times 11,9\times 9,8\times 8,7\times 7,6\times 6,4\times 4,2\times 2\}\right)=17$ since:

• The task $8\times 8$ cannot contribute since a gap of 3 cannot be filled by the unique candidate the task $2\times 2$.

• The task $6\times 6$ can also not contribute since a gap of 5 cannot be completely filled by the candidates $4\times 4$ and $2\times 2$.

The longest close hole ${\mathrm{𝑙𝑐𝑚𝑎𝑥}}_0^{11}\left(\{11\times 11,9\times 9,8\times 8,7\times 7,6\times 6,4\times 4,2\times 2\}\right)=15$: it corresponds to the longest time interval on which the resource is saturated by the illustrated placement and such that one bound of the interval does not intersect any tasks.

Second, consider a task of size $3\times 2$. Part (B) of Figure 3.7.20 provides a cumulative placement corresponding to the longest open hole problem according to $ϵ=11$ and $\sigma =20$. The longest open hole ${\mathrm{𝑙𝑚𝑎𝑥}}_{20}^{11}\left(\{3\times 2\}\right)=2$.

Figure 3.7.20. Two examples for illustrating the longest open hole problem: (A) a first instance with seven tasks of size $11\times 11$, $9\times 9$, $8\times 8$, $7\times 7$, $6\times 6$, $4\times 4$, $2\times 2$ with a slack $\sigma =0$ and a gap of 11, (B) a second instance with a single task of size $3\times 2$ with a slack $\sigma =20$ and a gap of 11.

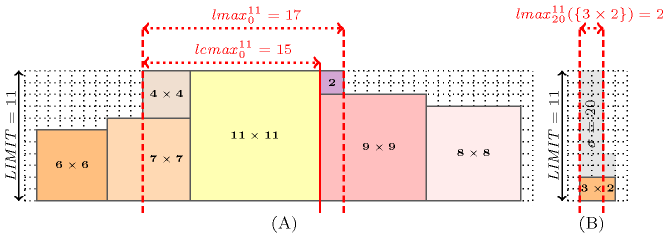
Figure 3.7.21 provides examples of the longest closed hole when we have 15 squares of sizes $1,2,\cdots ,15$ and a zero slack. Parts (A), (B),...,(O) respectively give a solution achieving the longest closed hole for a gap of $1,2,\cdots ,15$. For comparison, Figure 3.7.22 provides the same examples of the longest open hole with zero slack.

Figure 3.7.21. Given 15 tasks of sizes $1\times 1,2\times 2,...,15\times 15$ and a slack $\sigma =0$, examples of longest closed holes (in red) for a gap of $1,2,...,15$

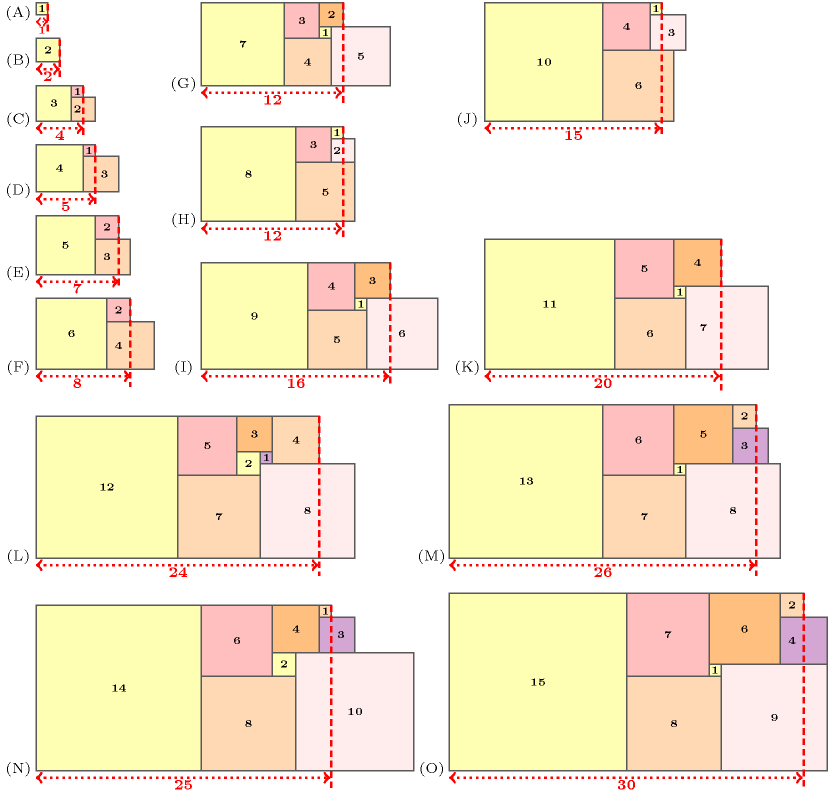
Figure 3.7.22. Given 15 tasks of sizes $1\times 1,2\times 2,...,15\times 15$ and a slack $\sigma =0$, examples of longest open holes (in red) for a gap of $1,2,...,15$