3.7.139. Logigraphe
modelling: logigraphe A constraint which can be used for modelling the logigraphe problem. The logigraphe problem, see Figure 3.7.38 for an instance taken from [Pitrat08], consists of colouring a board of squares in black or white, so that each row and each column contains a specific number of sequences of black squares of given size. A sequence of integers enforces:
a first block of consecutive black squares,
a second block of consecutive black squares,
.............................................,
a last block of consecutive black squares.
Each block of consecutive black squares must be separated by at least one white square. Finally, white squares may possibly precede (respectively follow) the first (respectively the last) block of black squares. The logigraphe problem is NP-complete [UedaNagao96].
Figure 3.7.38. Part (A): an instance of a logigraphe and the initial deductions achieved after posting the constraints, Part (B): the corresponding unique solution.
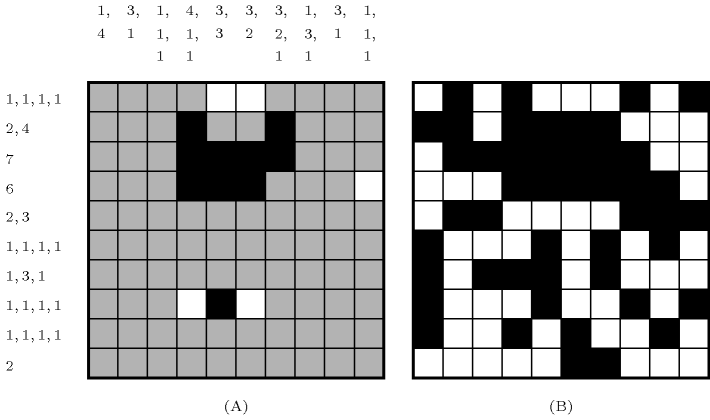
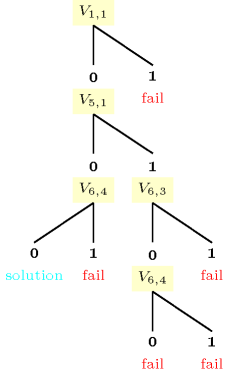
Part (A) of Figure 3.7.38 shows an instance of a logigraphe and the corresponding initial deductions achieved after posting the constraints associated with each row and each column. We assume that each constraint achieves arc-consistency, which is actually the case when the constraint is represented as a counter free automaton. A white or black square indicates an initial deduction (i.e., setting a variable to 0 or to 1). Part (B) of Figure 3.7.38 provides the unique solution found after developing three choices,Each time we try to assign a value to a not yet fixed variable, the number of choices is incremented by 1 just before making the assignment. assuming that variables are assigned from the uppermost to the lowermost row. Within a given row, variables are assigned from the leftmost to the rightmost column. Value 0 is tried first before value 1. Seven additional choices are required for proving that this solution is unique. Figure 3.7.39 displays the corresponding search tree. Within this figure, a variable denotes the 0-1 variable associated with the row and the column of the board.
Figure 3.7.39. Search tree developed for the logigraphe instance of Figure 3.7.38 (variables that are fixed by propagation were removed from the search tree)