3.7.247. Strong bridge

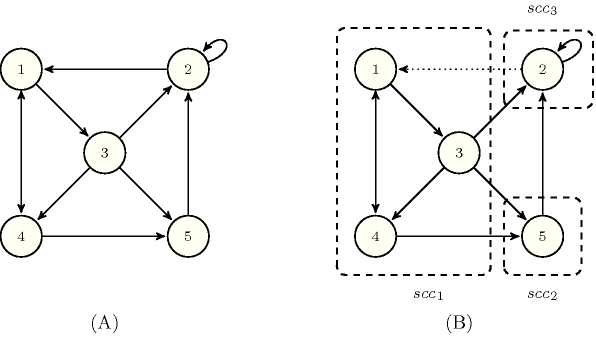
A constraint for which the filtering algorithm may use the notion of strong bridge (i.e., enforce arcs corresponding to strong bridges to be part of the solution in order to avoid creating too many strongly connected components). A strong bridge of a strongly connected digraph G is an arc such that, if we remove it, G is broken into at least two strongly connected components. FigureΒ 3.7.76 illustrates the notion of strong bridge on the digraph depicted by partΒ (A). The arc from the vertex labelled by 2 to the vertex labelled by 1 is a strong bridge since its removal creates the three strongly connected components depicted by partΒ (B) (i.e., the first, second and third strongly connected components correspond respectively to the sets of vertices {1,3,4}, {2} and {5}). The other strong bridges of the digraph depicted by partΒ (A) are the arcs 1β†’3 and 5β†’2. From an algorithmic point of view, it was shown inΒ [ItalianoLauraSantaroni10] how to compute all the strong bridges of a digraph G in linear time with respect to the number of arcs of G.

Figure 3.7.76. (A)Β A connected digraph, (B)Β its three strongly connected components 𝑠𝑐𝑐 1 , 𝑠𝑐𝑐 2 and 𝑠𝑐𝑐 3 when one of its strong bridge, the arc 2β†’1, is removed
ctrs/preface-214-tikz