3.7.175. Orthotope
Figure 3.7.46. Illustration of the notion of orthotope for various number of dimensions

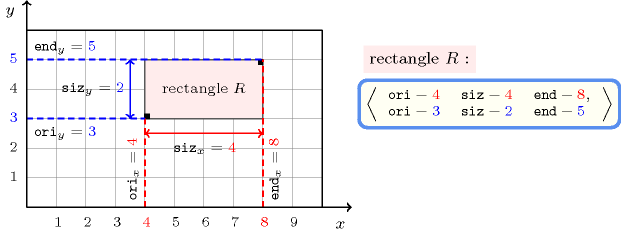
A constraint involving orthotopes. An orthotope corresponds to the generalisation of the rectangle and box to the -dimensional case. In addition its sides are parallel to the axes of the placement space. Figure 3.7.46 illustrates the notion of orthotope for and 4. A collection usually named , declared as , defines for each dimension (with ) the coordinate of its lower corner, the size and the coordinate of its upper corner in dimension . Figure 3.7.47 illustrates the representation of an orthotope for .
Figure 3.7.47. Representation of an orthotope when the number of dimensions in term of the collection