• $\mathrm{𝚊𝚜𝚜𝚒𝚐𝚗}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚌𝚘𝚞𝚗𝚝𝚜}$ (attribute $\mathrm{𝚋𝚒𝚗}$ of $\mathrm{𝙸𝚃𝙴𝙼𝚂}$ collection),

• $\mathrm{𝚊𝚜𝚜𝚒𝚐𝚗}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚗𝚟𝚊𝚕𝚞𝚎𝚜}$ (attribute $\mathrm{𝚋𝚒𝚗}$ of $\mathrm{𝙸𝚃𝙴𝙼𝚂}$ collection),

• $\mathrm{𝚋𝚒𝚗}\_\mathrm{𝚙𝚊𝚌𝚔𝚒𝚗𝚐}$ (attribute $\mathrm{𝚋𝚒𝚗}$ of $\mathrm{𝙸𝚃𝙴𝙼𝚂}$ collection),

• $\mathrm{𝚋𝚒𝚗}\_\mathrm{𝚙𝚊𝚌𝚔𝚒𝚗𝚐}\_\mathrm{𝚌𝚊𝚙𝚊}$ (attribute $\mathrm{𝚋𝚒𝚗}$ of $\mathrm{𝙸𝚃𝙴𝙼𝚂}$ collection),

• $\mathrm{𝚌𝚊𝚕𝚎𝚗𝚍𝚊𝚛}$ (attribute $\mathrm{𝚖𝚊𝚌𝚑𝚒𝚗𝚎}$ of $\mathrm{𝙸𝙽𝚂𝚃𝙰𝙽𝚃𝚂}$ collection),

• $\mathrm{𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍}\_\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜}$ (attribute $\mathrm{𝚖𝚊𝚌𝚑𝚒𝚗𝚎}$ of $\mathrm{𝚃𝙰𝚂𝙺𝚂}$ collection),

• $\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜}$ (attribute $\mathrm{𝚖𝚊𝚌𝚑𝚒𝚗𝚎}$ of $\mathrm{𝚃𝙰𝚂𝙺𝚂}$ collection),

• $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ (attribute $\mathrm{𝚘𝚛𝚒}$ of $\mathrm{𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴}$ collection for which $\mathrm{𝚜𝚒𝚣}=1$),

• $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ (attribute $𝚡$ of $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}$ collection for which $𝚕=1$),

• $\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}$ (attribute $𝚡$ of $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}$ collection for which $𝚕=1$),

• $\mathrm{𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚌𝚘𝚞𝚗𝚝}$ (attribute $\mathrm{𝚘𝚛𝚒𝚐𝚒𝚗}$ of $\mathrm{𝚃𝙰𝚂𝙺𝚂}$ collection),

• $\mathrm{𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚜𝚞𝚖}$ (attribute $\mathrm{𝚘𝚛𝚒𝚐𝚒𝚗}$ of $\mathrm{𝚃𝙰𝚂𝙺𝚂}$ collection).

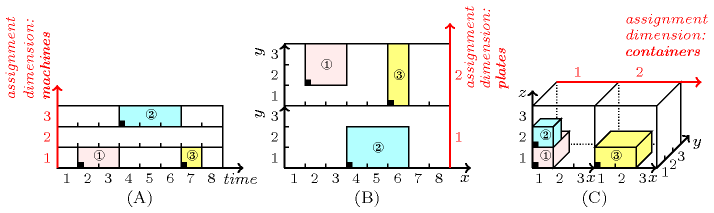
A constraint for handling placement problems involving orthotopes, where one of the dimensions of the placement space is so called an assignment dimension (i.e., one of the attributes of a collection passed as argument indicates the assignment dimension — the attribute is shown in parenthesis for each constraint). In order to illustrate the notion of assignment dimension let us first introduce three typical examples described in Figure 3.7.2:

• Part (A) of Figure 3.7.2 considers a scheduling problem where we have both to assign a task to a machine and to fix its start to a time-point, in such a way that two tasks that overlap in time are not assigned to the same machine. In this context the different potential machines where tasks can be assigned is called an assignment dimension. This problem can be directly modelled by a $\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜}$, a $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ or a $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ constraint. The corresponding three ground instances encoding the example are (attributes related to the assignment dimension are shown in bold):

  • $\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜}$$($

       $\langle \mathrm{𝚖𝚊𝚌𝚑𝚒𝚗𝚎}-\mathbf{1}\mathrm{𝚘𝚛𝚒𝚐𝚒𝚗}-2\mathrm{𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗}-2\mathrm{𝚎𝚗𝚍}-4\mathrm{𝚑𝚎𝚒𝚐𝚑𝚝}-1,$

        $\mathrm{𝚖𝚊𝚌𝚑𝚒𝚗𝚎}-\mathbf{3}\mathrm{𝚘𝚛𝚒𝚐𝚒𝚗}-4\mathrm{𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗}-3\mathrm{𝚎𝚗𝚍}-7\mathrm{𝚑𝚎𝚒𝚐𝚑𝚝}-1,$

        $\mathrm{𝚖𝚊𝚌𝚑𝚒𝚗𝚎}-\mathbf{1}\mathrm{𝚘𝚛𝚒𝚐𝚒𝚗}-7\mathrm{𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗}-1\mathrm{𝚎𝚗𝚍}-8\mathrm{𝚑𝚎𝚒𝚐𝚑𝚝}-1\rangle ,$

       $\langle \mathrm{𝚒𝚍}-\mathbf{1}\mathrm{𝚌𝚊𝚙𝚊𝚌𝚒𝚝𝚢}-\mathbf{1},$

        $\mathrm{𝚒𝚍}-\mathbf{2}\mathrm{𝚌𝚊𝚙𝚊𝚌𝚒𝚝𝚢}-\mathbf{1},$

        $\mathrm{𝚒𝚍}-\mathbf{3}\mathrm{𝚌𝚊𝚙𝚊𝚌𝚒𝚝𝚢}-\mathbf{1}\rangle )$

  • $\mathrm{𝚍𝚒𝚏𝚏𝚗}$$($

       $\langle \mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-2\mathrm{𝚜𝚒𝚣}-2\mathrm{𝚎𝚗𝚍}-4,\mathrm{𝚘𝚛𝚒}-\mathbf{1}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{2}\rangle ,$

        $\mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-4\mathrm{𝚜𝚒𝚣}-3\mathrm{𝚎𝚗𝚍}-7,\mathrm{𝚘𝚛𝚒}-\mathbf{3}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{4}\rangle ,$

        $\mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-7\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-8,\mathrm{𝚘𝚛𝚒}-\mathbf{1}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{2}\rangle \rangle )$

  • $\mathrm{𝚐𝚎𝚘𝚜𝚝}$$(2,\langle \mathrm{𝚘𝚒𝚍}-1\mathrm{𝚜𝚒𝚍}-1𝚡-\langle 2,\mathbf{1}\rangle ,$

               $\mathrm{𝚘𝚒𝚍}-2\mathrm{𝚜𝚒𝚍}-2𝚡-\langle 4,\mathbf{3}\rangle ,$

               $\mathrm{𝚘𝚒𝚍}-3\mathrm{𝚜𝚒𝚍}-3𝚡-\langle 7,\mathbf{1}\rangle \rangle$

              $\langle \mathrm{𝚜𝚒𝚍}-1𝚝-\langle 0,\mathbf{0}\rangle 𝚕-\langle 2,\mathbf{1}\rangle ,$

               $\mathrm{𝚜𝚒𝚍}-2𝚝-\langle 0,\mathbf{0}\rangle 𝚕-\langle 3,\mathbf{1}\rangle ,$

               $\mathrm{𝚜𝚒𝚍}-3𝚝-\langle 0,\mathbf{0}\rangle 𝚕-\langle 1,\mathbf{1}\rangle \rangle )$

• Part (B) of Figure 3.7.2 considers a placement problem where we have both to assign a rectangle to a rectangular piece and to locate it within the selected rectangular piece. In this context the different potential rectangular pieces where rectangles can be placed is also called an assignment dimension. Note that in such placement problems the size of an object in an assignment dimension is always equal to one. This problem can be directly modelled by a $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ or a $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ constraint. The corresponding two ground instances encoding the example are (attributes related to the assignment dimension are shown in bold):

  • $\mathrm{𝚍𝚒𝚏𝚏𝚗}$$(\langle \mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-\mathbf{2}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{3},$

                      $\mathrm{𝚘𝚛𝚒}-2\mathrm{𝚜𝚒𝚣}-2\mathrm{𝚎𝚗𝚍}-4,$

                      $\mathrm{𝚘𝚛𝚒}-2\mathrm{𝚜𝚒𝚣}-2\mathrm{𝚎𝚗𝚍}-4\rangle ,$

             $\mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-\mathbf{1}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{2},$

                      $\mathrm{𝚘𝚛𝚒}-3\mathrm{𝚜𝚒𝚣}-3\mathrm{𝚎𝚗𝚍}-6,$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-2\mathrm{𝚎𝚗𝚍}-3\rangle ,$

             $\mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-\mathbf{2}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{3},$

                      $\mathrm{𝚘𝚛𝚒}-6\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-7,$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-3\mathrm{𝚎𝚗𝚍}-4\rangle \rangle )$

  • $\mathrm{𝚐𝚎𝚘𝚜𝚝}$$(3,\langle \mathrm{𝚘𝚒𝚍}-1\mathrm{𝚜𝚒𝚍}-1𝚡-\langle \mathbf{2},2,2\rangle ,$

               $\mathrm{𝚘𝚒𝚍}-2\mathrm{𝚜𝚒𝚍}-2𝚡-\langle \mathbf{1},3,1\rangle ,$

               $\mathrm{𝚘𝚒𝚍}-3\mathrm{𝚜𝚒𝚍}-3𝚡-\langle \mathbf{2},6,1\rangle \rangle$

              $\langle \mathrm{𝚜𝚒𝚍}-1𝚝-\langle \mathbf{0},0,0\rangle 𝚕-\langle \mathbf{1},2,2\rangle ,$

               $\mathrm{𝚜𝚒𝚍}-2𝚝-\langle \mathbf{0},0,0\rangle 𝚕-\langle \mathbf{1},3,2\rangle ,$

               $\mathrm{𝚜𝚒𝚍}-3𝚝-\langle \mathbf{0},0,0\rangle 𝚕-\langle \mathbf{1},1,3\rangle \rangle )$

• Part (C) of Figure 3.7.2 considers a placement problem where we have both to assign a box to a  container and to place it within the selected  container. In this context the different potential  containers where boxes can be packed is also called an assignment dimension. Note that in such placement problems the size of an object in an assignment dimension is always equal to one. This problem can be directly modelled by a $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ or a $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ constraint. The corresponding two ground instances encoding the example are (attributes related to the assignment dimension are shown in bold):

  • $\mathrm{𝚍𝚒𝚏𝚏𝚗}$$(\langle \mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-\mathbf{1}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{2},$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-2,$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-2\mathrm{𝚎𝚗𝚍}-3,$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-2\rangle ,$

             $\mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-\mathbf{1}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{2},$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-2,$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-2,$

                      $\mathrm{𝚘𝚛𝚒}-2\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-3\rangle ,$

             $\mathrm{𝚘𝚛𝚝𝚑}-\langle \mathrm{𝚘𝚛𝚒}-\mathbf{2}\mathrm{𝚜𝚒𝚣}-\mathbf{1}\mathrm{𝚎𝚗𝚍}-\mathbf{3},$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-2\mathrm{𝚎𝚗𝚍}-3,$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-2\mathrm{𝚎𝚗𝚍}-3,$

                      $\mathrm{𝚘𝚛𝚒}-1\mathrm{𝚜𝚒𝚣}-1\mathrm{𝚎𝚗𝚍}-2\rangle \rangle )$

  • $\mathrm{𝚐𝚎𝚘𝚜𝚝}$$(4,\langle \mathrm{𝚘𝚒𝚍}-1\mathrm{𝚜𝚒𝚍}-1𝚡-\langle \mathbf{1},1,1,1\rangle ,$

               $\mathrm{𝚘𝚒𝚍}-2\mathrm{𝚜𝚒𝚍}-2𝚡-\langle \mathbf{1},1,1,2\rangle ,$

               $\mathrm{𝚘𝚒𝚍}-3\mathrm{𝚜𝚒𝚍}-3𝚡-\langle \mathbf{2},1,1,1\rangle \rangle$

              $\langle \mathrm{𝚜𝚒𝚍}-1𝚝-\langle \mathbf{0},0,0,0\rangle 𝚕-\langle \mathbf{1},1,2,1\rangle ,$

               $\mathrm{𝚜𝚒𝚍}-2𝚝-\langle \mathbf{0},0,0,0\rangle 𝚕-\langle \mathbf{1},1,1,1\rangle ,$

               $\mathrm{𝚜𝚒𝚍}-3𝚝-\langle \mathbf{0},0,0,0\rangle 𝚕-\langle \mathbf{1},2,2,1\rangle \rangle )$

In summary, within the context of placement problems that use a constraint like $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ or $\mathrm{𝚐𝚎𝚘𝚜𝚝}$, the coordinate of an object in the assignment dimension corresponds to the resource to which the object is assigned. Note that the size of an object in the assignment dimension is always set to 1. This stems from the fact that an object is assigned to a single resource.

Figure 3.7.2. Three illustrations of the notion of assignment dimension where the assignment dimension is shown in red

Using constraints like $\mathrm{𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍}\_\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜}$, $\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜}$, $\mathrm{𝚍𝚒𝚏𝚏𝚗}$, $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ or $\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}$ allows to model directly with a single global constraint such problems without knowing in advance to which machine, to which rectangular piece, to which container, a task, a rectangle, a box will be assigned. For each object the potential values of its assignment variable provide the machines, the rectangular pieces, the  containers to which the object can possibly be assigned. Note that this allows to avoid 0-1 variables for modelling such problems.

Within constraints like $\mathrm{𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚌𝚘𝚞𝚗𝚝}$ or $\mathrm{𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚜𝚞𝚖}$ the concept of assignment dimension is extended from the fact that a variable is assigned a value to the fact that a variable is assigned an interval (i.e., a value in an interval).